 Práce s bakalářkou se rozrostla do nečekaných rozměrů a já si musel ujasnit pár priorit. Nu, překlenul jsem jeden z nejhorších (prozatím) bodů, tak jsem si řekl, že bych to tu za odměnu mohl trochu oživit. 🙂 Přecijen někteří z vás tento týden píší.
Práce s bakalářkou se rozrostla do nečekaných rozměrů a já si musel ujasnit pár priorit. Nu, překlenul jsem jeden z nejhorších (prozatím) bodů, tak jsem si řekl, že bych to tu za odměnu mohl trochu oživit. 🙂 Přecijen někteří z vás tento týden píší.
Ti šťastnější až v pátek. Avšak na programu otázek je pouze 1. úloha KVDR momenty a 2-4. úloha tah/tlak (SU i SN), vše z toho již bylo probráno zde. Jen mne mrzí, že jsem nestihl nějaké příklady.
Co dnes probereme. Budeme pokračovat v tahu/tlaku ~ prutových soustav.
Obsah článku
Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [9] – 05.3.2013 – Fuis: >> [MP3] <<
Prutová soustava
O jakou soustavu prutů se jedná? O složení, kde:
- jsou pruty spojené k sobě rotačními vazbami a následkem toho zde není moment
- soustava splňuje vnitřní nepohyblivost
Na začátek 2 příklady, kdy podmínky splněny nejsou a nejedná se o prutovou soustavu:

Vlevo: Pokud zabereme silami, celá sestava se zhroutí.
Vpravo: Pokud zabereme silami, soustava se nezhroutí, avšak přibudou momenty.
Plně 100% a bezchybná soustava, která nepřenáší žádný moment (pouze tah/tlak, protože je složena jen z binárně zatížených členů), je např:
Prut. soustavy staticky neurčité
Svět však není tak shovívavý, aby nám dopřál počítání bez deformačních podmínek a tak existují -převážně- staticky neurčité úlohy. Proč? Už jsme si to řekli v nějaké x-té lekci. Čím více (v rozumné míře) staticky neurčitá úloha, tím lepší má únosnost / stabilitu a další parametry. Takový rám kola je myslím 9x (nebo 6x) staticky neurčitý. To je pak rovnic 🙂
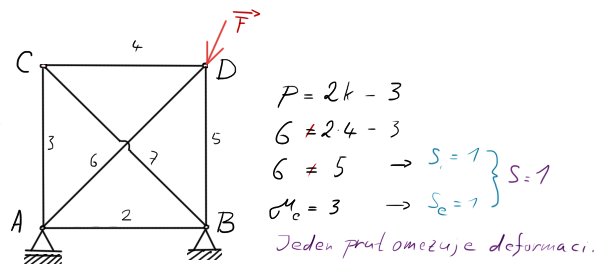
Vnější SN
Neboli: Omezení deformace vnějšími vazbami

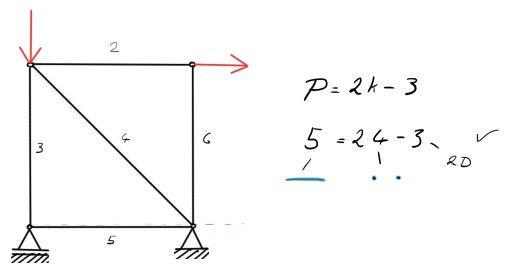
$\mu = 3$ … počet neznámých parametrů: $\{F_A, F_B, F_D\}$.
$\nu = 2$ … počet možných podmínek.
$S_e = \mu – \nu = 1$ … 1x staticky externě neurčitá.
Protože se jedná o prutovou soustavu, která obsahuje jen binárně zatížené členy, může být počet neznámých $\mu$ vždy jen 1 / vazba.
Napíšeme tedy počet neznámých $\mu = 3$, počet možných $\nu = 2$ (v prutové soustavě není moment). Vyjde nám to jednou staticky neurčité. Co s tím? máme dvě možnost. Ta méně pěkná je zde:
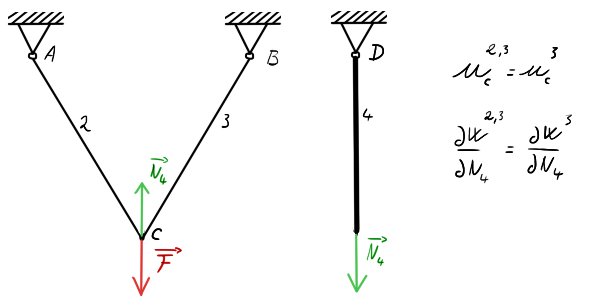
ČÚ a následné rozdělení na 2 tělesa
Řeším tak pak rovnice pro oba stavy a budu muset psát 2 Castiglianovy věty.
Snazší řešení je však:
ČÚ s uvolněním jedné z vazeb
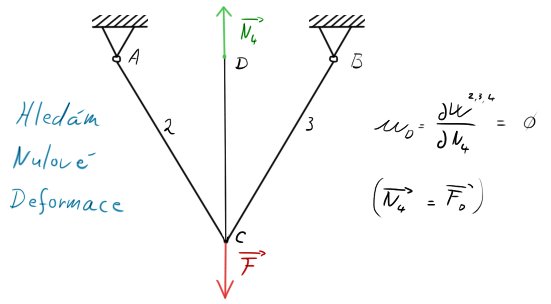
Posunutí v bodě $D$ je rovnou parciální derivaci energie napjatosti $W$ z prutů $2, 3, 4$ dle síly normálové $N_4$.
DP: $N_4 = F_D$
Zde už pěkně jen jeden Castiglian. Vyřeším jím sílu $N_4$ (potažmo $F_D$) a zbytek už je jen o doplnění do rovnic SR.
Info
Jakou vazbu si mám vybrat a uvolnit? V tomto případě je to jedno. Avšak řídíme se pravidlem, že vždy uvolňujeme vazbu, která je tak nějak nejvíce/nejméně sympatická. Je něčím odlišná, přímo excentrická! 🙂
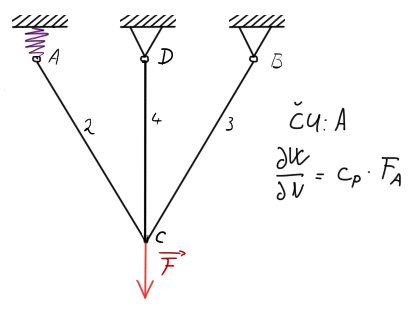
Pokud by třeba byla vazba $A$ pružina a ne rotační vazba, jako na obr:
Uvolníme právě tuto vazbu s pružinou (a bod $D$ necháme s nezájmem být), provedeme částečné uvolnění a Castiglianovu větu sestrojíme s pamatovákem na pružinu, neboli $c_p \cdot F_A$. Už to nebude posunutí $u=0$.
To samé by platilo, pokud by se jednalo o:
- ohřátí (přesah)
- prut by byl delší (přesah)
- prut by byl kratší (vůle)
- ochlazení (vůle)
Vnitřní SN
Co však vnitřní SN, neboli pokud přidáme navíc jeden prut, který bude omezovat deformaci uvnitř.
Opět, jak už to bývá u všeho staticky neurčitého, částečně uvolníme a vyjmeme ze soustavy pryč.
Zde si musíme dát pozor na znamínko. Castiglian hovoří jasně. Pokud je to po směru pohybu, je to plus, pokud proti směru pohybu, je to mínus.
Energie napjatosti celé soustavy je pak:
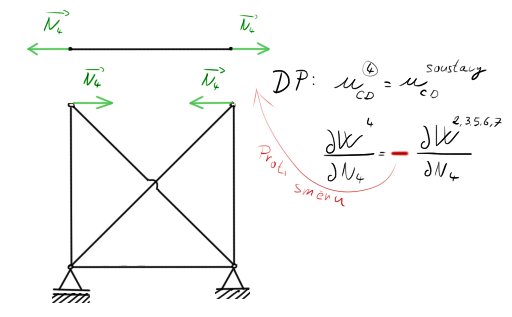
$$\dfrac{\partial W^4}{\partial N_4} + \dfrac{\partial W^{2, 3, 5, 6, 7}}{\partial N_4} = 0$$
A tomu odpovídá částečné uvolnění:
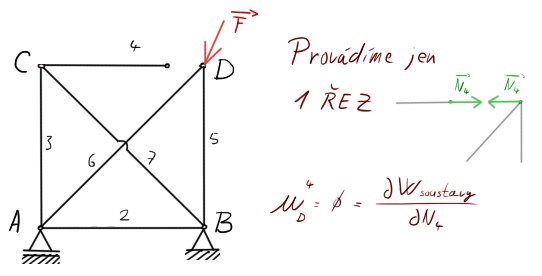
Budeme tedy provádět vždy jen jeden řez, nebudeme z tělesa nic odjímat a Castiglian se bude = 0. Derivujeme tedy vždy energii napjatosti celé soustavy ku derivaci síly ve vlákně řezaného prutu.
Pokud byste zapomenuli, co se vlastně skrývá pod energií napjatosti, nedivil bych se. Zde tedy pro připomenutí:
$$\dfrac{\partial W_{soustavy}}{\partial N_4}=\sum_{1}^{n}{\dfrac{N_i l_i}{E_i S_i}} = \dfrac{N_1 l_1}{ES_1}+\dfrac{N_2 l_2}{ES_2}+\dfrac{N_3 l_3}{ES_3}+\dfrac{N_4 l_4}{ES_4}+\dfrac{N_5 l_5}{ES_5}+\dfrac{N_6 l_6}{ES_6}+\dfrac{N_7 l_7}{ES_7} $$
Kde:
- $E$ … modul tuhosti průřezu v tahu $[MPa]$
- $S$ … obsah plochy průřezu $[mm^2]$
- $l$ … délka prutu $[mm]$
- $N$ … hodnota tahové síly v prutu $[N]$
Info
Opět upozorňuji, pokud by byla v soustavě pružina, volíme prut, který má s touto pružinou co dočinění. Zjednoduší se nám pak Castiglian na tento tvar:
Tuhé tělesa
Tuhé tělesa se nám budou líbit. Proč? Protože je většinou bereme jako „stěnu“ nebo něco, co se nám vůbec nedeformuje (oproti ostatním prutům).
Příklad takového tuhého tělesa by mohla být sirka, pokud se ji budeme snažit ohnout tím, že na ni upevníme 2 vlákna vlasů a budeme tahat. Vlasy se jistojistě (doufám :-D) přetrhnou o dost rychleji, než by se stačila sirka ohnout, ne-li přímo rupnout. Považujeme tedy sirku za tuhé těleso a počítáme pouze a jen vlasy.
Pokud však budeme sirkou(kami) tlačit do ocelové tyčky, bude to právě sirka, kterou budeme zkoumat a ocelová tyčka bude tuhé těleso.
Pokud však budeme s naší ocelovou tyčkou machrovat, že udrží dům ve vzduchu, budem onen dům tuhé těleso a tyčka se prodlouží a praskne.
Je to relativní 🙂 Pokud nám tedy ve škole řeknou, že se jedná o tuhé těleso, nemusíme ho zahrnovat do výpočtu a bereme ho tak, jak leží a stojí. (V praxi ho buď započítáváme, nebo s podstatnými argumenty odstraníme z výpočtů, ale musíme objasnit, proč jsme tak udělali.)
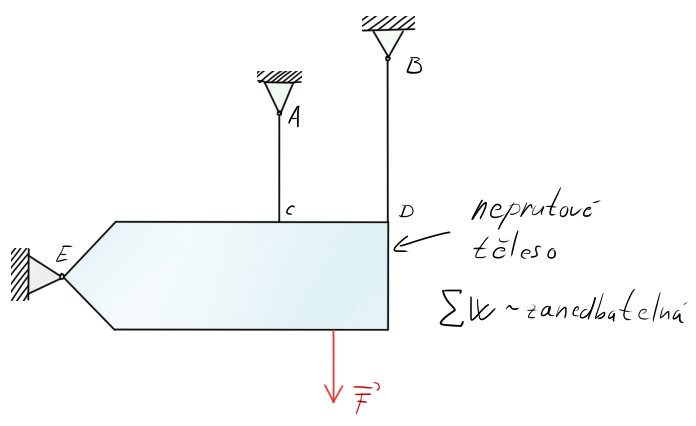
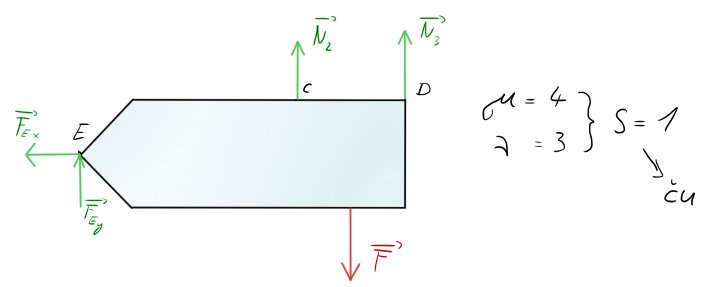
Uveďme si příklad:
Dalším postupem je už klasicky úplné uvolnění.
Zde vidíme, že těleso vyšlo 1 x SN.
Nezbývá nám tedy, než částečně uvolnit.
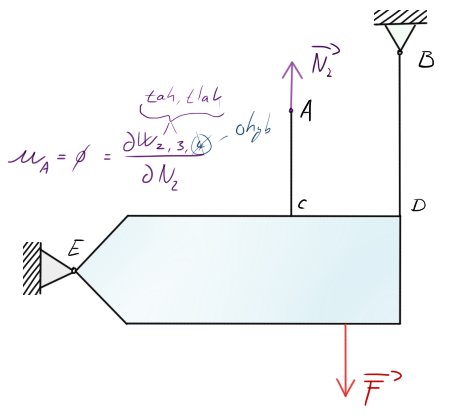
Nevidíme zde žádné „viditelné nápadné“ pruty jako třeba ohřátí, prodloužení, ochlazení, zkrácení, nebo pružinu, protože je naprosto čistě na nás, jakou si zvolíme sílu a částečně ji uvolníme. Nedoporučuji moc rotační vazby a pokud je tam někde tah / tlak, tak do něj 🙂
Z Castiglianovy věty, kdy jsme si určili, že posuv bodu $A$ bude nulový, jsme vyřešili sílu $N_2 = F_A$ a dále už můžeme postupovat klasickými rovnicemi statické rovnováhy. $(\sum x = 0\ |\ \sum y = 0\ |\ \sum M_{o_E} = 0)$
Tím dostaneme zbylé síly $F_B, F_{Ex}, F_{Ey}$ a můžeme určovat další parametry, které by nám úloha dala. Například prodloužení či bezpečnost a jiné.
Pro dnešek tedy vše a příště se vrhneme na prostý ohyb.

13 responses to “PPI – 09 – prutové soustavy”