 Dnešní přednáška byla prakticky jen a jen o prostém tahu / tlaku a teorii v ní obsažené. Pro běžné smrtelníky je důležité si z ní odnést tak 2 vzorce, ale pro nás zvídavější by se vyplatilo pochopit, jak to tam vlastně funguje a jak to rozlišit od ohybu či smyku, který přijde, ať chceme nebo ne. 🙂
Dnešní přednáška byla prakticky jen a jen o prostém tahu / tlaku a teorii v ní obsažené. Pro běžné smrtelníky je důležité si z ní odnést tak 2 vzorce, ale pro nás zvídavější by se vyplatilo pochopit, jak to tam vlastně funguje a jak to rozlišit od ohybu či smyku, který přijde, ať chceme nebo ne. 🙂
Při vysvětlování tahu/tlaku se také podíváme konečně na energii napjatosti, která se používá (a budeme ji i konkrétně konečně aplikovat) v Castiglianově větě. Poté se také seznámíme s další kružnicí, která náleží Mohrově rovině, a to kružnicí zobrazující obecné napětí v libovolném řezu. Neboli Mohrova kružnice obecného napětí.
Obsah článku
Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [6] – 21.2.2013 – Fuis: >> [MP3] <<
Začnu koncem (posledními 20 minutami) minulé hodiny. Neboli audio berte z přednášky > 5 < od nějaké 1hod 20min času.
Prostý tah / tlak
Aneb Dědeček, babička, pejsek, kočička, myšička i blecha tahají vodorovně lano.
Kdy ho budeme uvažovat
Uvažovat prostý tah / tlak můžeme jen u prutu, který bude splňovat následující podmínky:
• Přímý – bude to rovné
• Prizmatický – přímý prut konstantního průřezu, žádné změny geometrie
• Homogenní – prut, který je jen z jednoho materiálu ve všech místech stejný
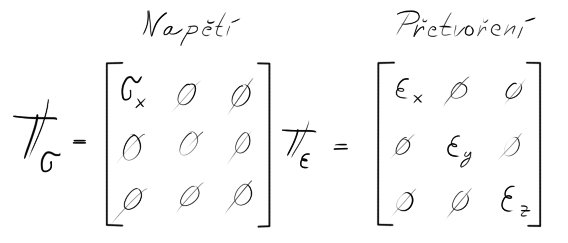
Tenzory přetvoření a napětí
Tenzor přetvoření a napětí pro obecné zatížení si jistě pamatujete, že? 🙂
U prostého tahu a tlaku se tenzory dají značně zjednodušit. Hurray! Pokud uvažujeme, že se jedná jen o působení v jedné ose, např. $x$:
Jak jednoduché, že? 🙂 Pokud působím v jedné ose, budu mít jen $\sigma_x$.
Avšak! proč mám trojosou deformaci? Protože pokud si představíte válec, který budeme v ose natahovat, bude se nejen prodlužovat, ale také (ideálně) uprostřed ztenčovat souměrně jak po ose $y$, tak i po ose $z$. Proto zapamatovat!
Pro jednoosou napjatost máme trojosou deformaci.
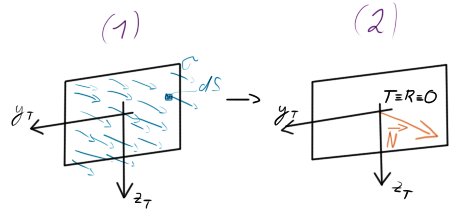
Rozložení napětí
Ze silové podmínky $N = \displaystyle \int_{\Psi} \sigma \ dS$, kterou můžeme zobrazit jako (1) můžeme statickou ekvivalencí nahradit všechny prvky napětí jedinou silou (2). Tato operace však platí pouze pro CSS!.
Pokud bychom měli jiný souřadný systém, přibyly by ještě nějaké lineární momenty.
Proč toto zmiňujeme? U prostého tahu budeme uvažovat, že normálová síla působí vždy v těžišti řezu a je ekvivalentní k napětí, které se v řezu vyskytuje. Řez také uvažujeme kolmý ke střednici.
Co kdyby nebyl kolmý? O tom se pobavíme na konci lekce.
Energie napjatosti
S energií napjatosti (dále jen E. napjatosti) jsme se už setkali, když jsme poprvé nakousli Castiglianovu větu. Je to jakási energie soustavy, která vychází z deformační energie.
Deformační energii můžeme napsat jako $W=\dfrac{1}{2} F \cdot u$, pro normálovou sílu můžeme přepsat na $W=\dfrac{1}{2} N \cdot u$.
Uděláme si lehké odvozování.
Pokud si vyjádřím, že normálová síla $N$ je napětí na plochu ($\sigma \cdot S$) a poté, že napětí $\sigma$ je vlastně tuhost násobená přetvořením ($E \cdot \varepsilon$), dostanu ve výsledku „jakousi“ energii napjatosti $W$ pro homogenní deformaci prutu.
Nás ale bude zajímat spíše elementární (mini mikro) část, neboli vypustíme objem $V$, nazveme ji měrnou energií napjatosti $\Lambda$.
A jestliže se tedy chceme dostat k obecné energii napjatosti $W$, jejíž „vzorec“ tedy můžeme aplikovat prakticky kamkoli (JEN! pro prostý Tah / Tlak), tak onu měrnou E. napjatosti $\Lambda$ integrujeme opět po objemu $dV$.
Pokud se vás tedy někdo bude ptát na obecnou E. napjatosti $W$ v tahu / tlaku, víte, co mu odpovědět. (to červené)
Deformace v Tahu / Tlaku
Deformaci lze řešit více způsoby. Dokonce i Hookovým zákonem. Nejzažitější jsou však dva:
- pokud mám 1 těleso -> pomocí E. napjatosti (případně složitěji přes Castigliana)
- pokud mám prutovou soustavu -> pomocí Castiglianovy věty
Info: Castigliana používáme -zásadně- u ohybu. U tahu určitě při prutové soustavě, ale pokud řeším jen jedno těleso, lze to řešit elegantněji.
Posunutí obecného bodu
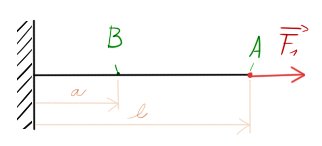
Jestliže mám vetknutý nosník (znázorněný na obrázku), který zatěžuji silou $F_1$, mohu si určit deformaci v jakémkoli jeho bodě. Protože se jedná o přímý, prizmatický, homogenní prut, deformace se projeví jen a pouze v ose $x$.
Budu se zajímat o dva body. Na konci v působišti síly $F_1$ ~ místo A a někde náhodně uvnitř, tj ~ místo B.
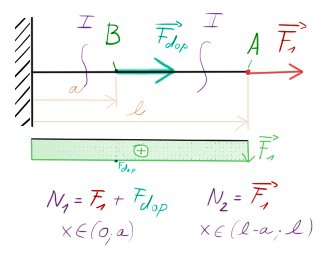
Abychom však zjistili posunutí v bodě B, kde nepůsobí žádná síla, musíme do toho bodu dát nějakou imaginární (vlastní/doplňkovou) sílu $F_{dop}$ a položit ji 0. K tomuto se v dalších lekcích ještě častokrát vrátíme, teď to berme jako skutečnost.
Nosník si tedy zatížím naší doplňkovou silou $F_{dop}$ (která je nulová: $F_{dop}=0 N$) a nakreslíme si průběh VVÚ.
Nejdříve si ještě připomeňme, jak se derivuje obecná funkce, která má nějaký exponent.
Místo A
Matika-magicka:
Zde bychom si mohli vyznačit několik postřehů:
- $F_{dop}$ v tomto vůbec nehrála roli
- posunutí je výsledkem normálových VVÚ po délce $l$
Místo B
Matika-magicka:
I zde si vyznačíme pár postřehů:
- $F_{dop}$ v tomto případě hrála velkou roli, parciálně se dle ní integrovalo, takže nám úplně vypadl člen, který se nacházel (od vetknutí) za intervalem, kde jsme přidali sílu doplňkovou
- posunutí je výsledkem normálových VVÚ po délce od vetknutí až k místu, které nás zajímá
Souhrn
Pokud tedy nebudeme počítat se soustavou prutových těles, Castiglianovu větu (uvedenou výše, neboli parciální derivace energie napjatosti vůči parciální derivaci síly) nemusíme použít a můžeme si případ velmi zjednodušit vzorcem:
$$\Delta l = \frac{N \cdot l}{E \ S}$$
Kde
• $N$ je VVÚ v bodě, které nás zajímá, směrem od nějaké vazby (většinou vetknutí), která bude mít v tom samém směru posuv nulový.
• $S$ je plocha průřezu kolmém na střednici.
• $E$ je tuhost tělesa (pro ocel počítáme $E = 210\ 000\ Mpa$).
• $l$ je vzdálenost od od místa vetknutí (či jiné vazby, která má nulový posuv ve stejném směru) až do místa, kde nás posuv zajímá.
Dodatek
Jak už jsme si řekli na začátku, jak je možné, že má jednoosá napjatost trojosou deformaci?
Pokud tahám jen normálovým napětím, jak je možné, že jsou tam plastické přeměny? (zúžený krček např)
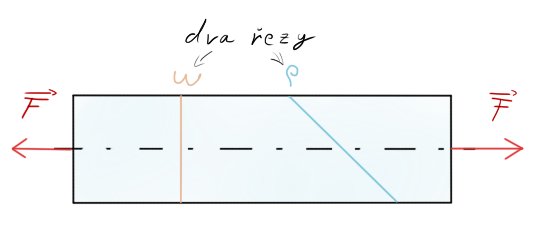
Všechny doposud probrané vzorce a vysvětlení vztahujeme k řezu kolmém k průřezu $\Psi$. Co by se však stalo, kdybychom těleso řízli pod nějakým úhlem $\alpha$? Představme si to konkrétně zde:
Působíme na trubku tahovou silou $F$. Řízneme ji v:
• řezu kolmém ~ $\omega$
• řezu po nějakým úhlem ~ $\rho$
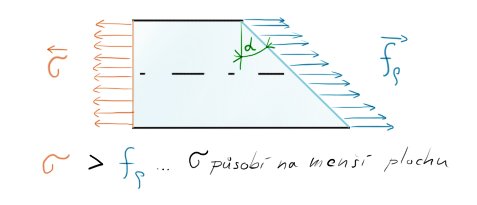
Zde můžeme spatřit, že v kolmém řezu působí (jak to známe) napětí $\sigma$, ale v šikmém (na větší ploše) působí jakési obecné napětí $f_{\rho}$, které nemá jen normálovou složku, ale je složeno i ze složky smykové.
Detail si ukážeme zde:
Zde tedy vidíme a máme dokázáno, že i když působíme na těleso pouze normálovým napětím, toto napětí se při jiných, než kolmých řezech, rozkládá na smykové složky, které poté způsobují plastické deformace (už se to nebude jen natahovat, ale třeba zužovat, rozšiřovat, atd).
Obecné napětí $f_{\rho}$ bychom si mohli společně s jeho normálovou složkou $\sigma_{\rho}$ a smykovou složkou $\tau_{\rho}$ vyjádřit jen pomocí napětí kolmého na průřez $\sigma$ a úhlu $\alpha$, pod kterým to působí.
Při dosazení různých úhlů můžeme pozorovat změny velikostí normálového a smykového napětí. Pokud bychom si vzali typické podezřelé úhly (0° 45° 90°), vytvoříme si jakousi tabulku, které nám poví něco o extrémech.
Extrémy funkcí
Pokud budeme uvažovat rovinu kolmou k průřezu, největší význam zde hraje normálové napětí. Jestliže však řez provedeme pod 45° (v Mohrově rovině 90°), zjistíme, že se zde najde i smykové napětí o velikosti půlky normálového. Smyk je však vždy nebezpečný. Jestliže řez nahneme o 90°, aby byl rovnoběžný s působící silou, nepůsobí zde nic.
Za předpokladu, že jsme dobří v matice a umíme všechno se vším vyjádřit, jsme schopni stvořit rovnici
Matika-magicka
Ta nám blízce může připomínat rovnici kružnice. A jak už jsme zkoumali v Mohrově rovině Mohrovu kružnici kvadratických momentů, zde budeme mít Mohrovu kružnici pro jednoosou napjatost.
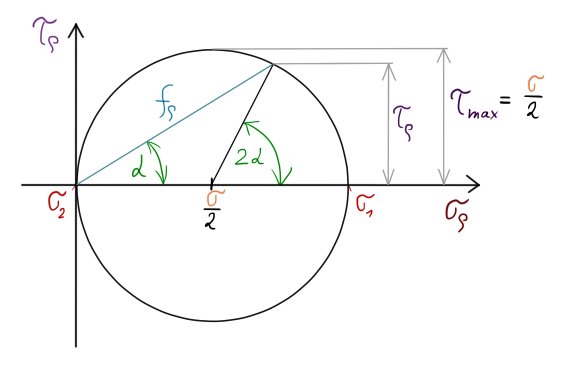
Mohrova kružnice pro jednoosou napjatost
O této kružnici se dá říct mnohé:
• Znázorňuje obecné napětí $f_{\rho}$ v libovolném řezu
• Jedna strana kružnice tečuje osu smykových napětí $\tau_{\rho}$ ~ v tomto bodě je napětí nulové
• Maximální normálové napětí $\sigma$ připadá bodu $\sigma_1$, který se vyskytuje při úhlu $0°$ (kolmý řez na střednici)
• Maximální smykové napětí $\tau$ připadá vršku kružnice a má velikost $\sigma/2$
• Znaménková konvence – pokud si v řezu namaluji vektor normály a smyku a poté vektor normály otočím po směru hodinových ručiček o 90°, platí, že pokud je normála shodná se smykovým vektorem, je smykové napětí kladné, pokud je normála opačná ke smykovému vektoru, je smykové napětí záporné.
Pro dnešek nejspíše vše, v úterý budeme pokračovat.
Čeká nás další pitvání prostého tahu a tlaku, koukneme se, co když bude těleso zahřáto, co když tam bude více sil, co v případě, že v něm bude vrub, nebo ho budem prodlužovat, ale jiné těleso nám tomu bude zamezovat a seznámíme se s konstrukční či funkční vůlí 🙂
Hawk




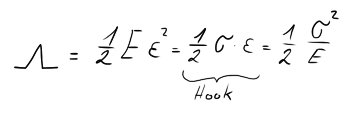
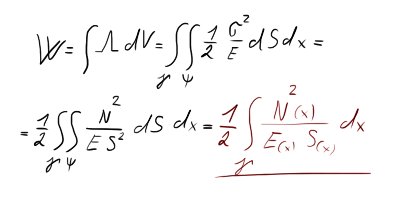

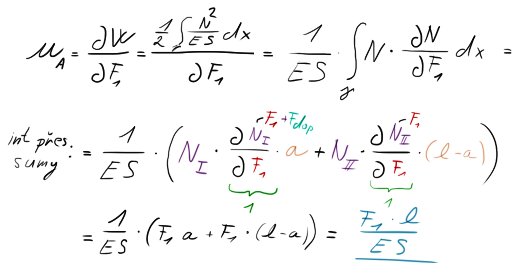
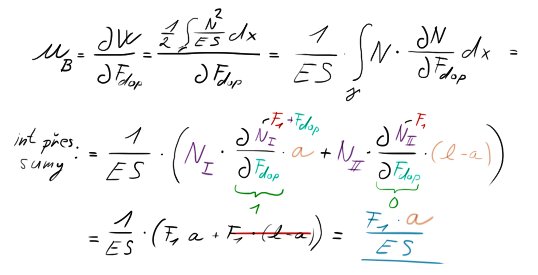
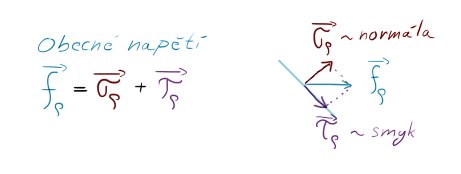
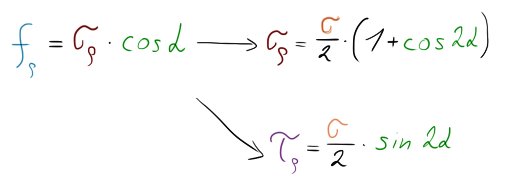
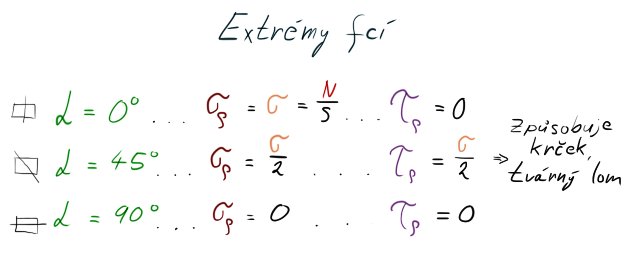
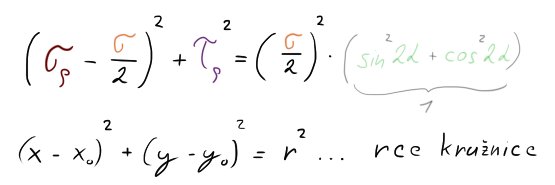
One response to “PPI – 06 – prostý tah/tlak, E. napjatosti, Castiglian, Mohrova kružnice”