 Konečně doháním nějaké ty časové ztráty, vše začínám nazpět stíhat, takže zde máte 8. lekci z Pružnosti Pevnosti.
Konečně doháním nějaké ty časové ztráty, vše začínám nazpět stíhat, takže zde máte 8. lekci z Pružnosti Pevnosti.
Dnes se budeme zabývat Staticky neurčitými úlohami, které načal na pan Fuis lekci nazpět, ale já se rozhodl to dát do jedné, aby to nebylo zbytečně rozkouskované.
Čeká nás tedy vysvětlení částečného uvolnění s následujícím osvojením různých deformačních podmínek, které mohou nastat u prostého tahu/tlaku. Nezapomeňte, že neřešíme stále nic jiného. U ohybu, krutu a smyku nám zas něco přibude, což však bude na jedno brdo, takže vnímat a pochopit teď, srovnat s novou látkou později 🙂
Obsah článku
Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [8] – 28.2.2013 – Fuis: >> [MP3] <<
Staticky neurčité úlohy
Jak poznat staticky neurčitou úlohu? Stejně jako ve statice.
První krok
Úlohu úplně uvolníme, neboli všechny vazby nahradíme neznámými silami dle stupňů volnosti. Poté určíme statickou neurčitost.
Pro ty, kteří si nepamatují postup:
Jestliže nám tedy vyjde, že je úloha několikráte staticky neurčitá, co nám to vlastně říká?
Jak už jsem se zmínil v předešlých lekcích, statická neurčitost snižuje napjatost a zvyšuje bezpečnost. Pokud budeme mít nosník položený na dvou rotačních vazbách a doprostřed bude působit síla, jistě bude bezpečnější, pokud i doprostřed dáme ještě nějakou podpěru.
Ovšem úloha bude 2x staticky neurčitá (2 rotační vazby – 4 neznámé, 1 podpěra – 1 neznámá, možné rovnice pro 2D úloha – 3. Neznámé – možné = stupeň ($\mu – \nu = s$), neboli 5 – 3 = 2)
Druhý krok
Úlohu částečně uvolníme, aneb z definice:
Uvolnění prutu s omezenými deformačními parametry na úroveň prutu bez omezení deformace (obvykle nepohyblivě uloženého) a sestavení deformačních podmínek.
Pro nás to tedy znamená, že místo jedné/dvou vazeb (dle stupně statické neurčitosti) umístíme na její místo sílu/moment (moment dávám třeba při ohybu / krutu zde však probíráme prozatím jen prostý tah/tlak, kde se přidává JEN síla) s příslušnou deformační podmínkou.
Příklad
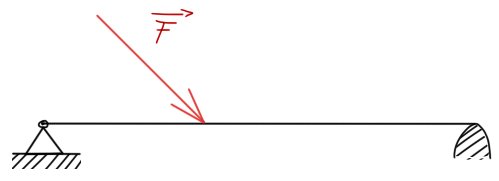
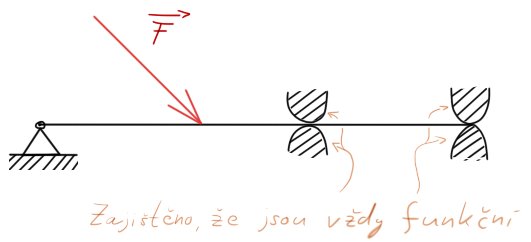
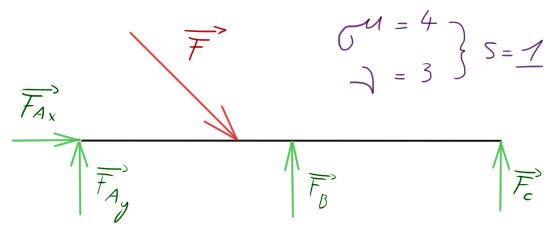
Na 1. obr. je zatížený prut, který je staticky určitý. Pod ním je prut 1x staticky neurčitý.
Důvod dvojice „vertikálních“ podpěrných vazeb je ten, abychom vyloučili nefunkčnost vazby. Neboli ať už by se to prohýbalo dolů či nahoru, jedna z nich bude vždy funkční.
Jak tedy správě postupovat?
Úplné uvolnění
Úlohu tedy celkově zbavíme veškerých vazeb, které nahradíme silami.
Díky tomuto uvolnění jsme schopni poznat dvě věci:
- Statickou neurčitost
- Nalézt všechny neznámé parametry a rozhodnout se (v případě SN, který z nich použiji do dalšího postupu)
Částečné uvolnění
Vidíme tedy, že je úroveň 1x staticky neurčitá. Zvolíme si tedy jednu z neznámých sil, kterou použijeme do dalšího postupu a přidáme k ní deformační podmínku. Zvolit si můžeme téměř jakoukoli z těchto čtyř.
Podíváme se na ně tedy podrobně:
- $F_C$ – pokud zvolíme tuto sílu, DP bude, že se průhyb musí rovnat nule (vertikální posun je nulový)
- $F_B$ – DP stejné jak u $F_C$. Průhyb $w=0$
- $F_{Ay}$ – ne tak častá volba (většinou se volí právě ony podpěry), jinak stejná DP: $w=0$
- $F_{Ax}$ – zde pozor. Opakuji – POZOR.
Jaký je tedy problém s $F_{Ax}$? Částečné uvolnění je uvolnění na úroveň statické určitosti, ne deformace. Co to znamená v našem rodném jazyce?
Pokud bychom nechali 3 vazby dole a žádnou vlevo/vpravo, síla $F$ nám může s nosníkem pohybovat. Co více, v y-ovém směru je tu jedna podpěra navíc, která je deformační. Proto pozor. Pokud je to možno, volte si jednoduché podpěrné vazby.
Zde uvádím veškeré případy uvolnění ve zvolených vazbách:

1. – 3. možnosti jsou v klidu. U 4. možnosti by se těleso pohybovalo doprava! Není zafixované a nelze to řešit.
Řešení SN u prostého tahu/tlaku
Projeďme si teď nějaké možné varianty SN úloh prutu s prostým tahem/tlakem.
Řešit budeme tento „vždy“ vetknutý prut mezi dvě pevné vazby.
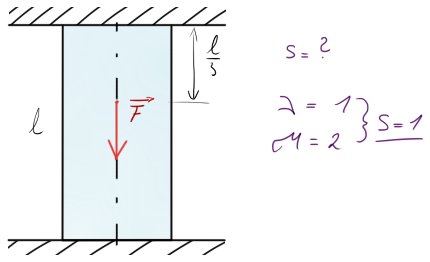
Proč $\nu = 1$? Nepůsobíme silou do stran, není zde přidaný moment, $F$ působí po ose. Můžeme si úlohu tedy „ulehčit“ z úlohy obecné na úlohu prostého tahu/tlaku a nahradit $\nu = 3$ za $\nu = 1$ a vazby $\mu = 6$ za $\mu = 2$.
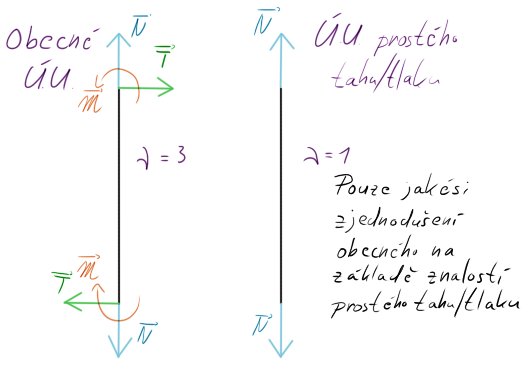
Jak vidíme, prut je 1x staticky neurčitý. Na ukázku si ho úplně uvolníme napřed obecně a poté s pohledem jen a pouze prostého tahu/tlaku.
Zde si všimneme obrovského zjednodušení. U prostého tahu/tlaku neuvažujeme smykové síly $T$, ani momenty $M$, proto prut úplně uvolníme jen s normálovými silami. Pozor! Při tomto předpokladu se nám zmenší možné podmínky ze tří na jednu.
Deformační podmínky
Deformační podmínky, alias podmínky, které napíšete k vazbě, kde provedete ČU.
Tuhá vazba
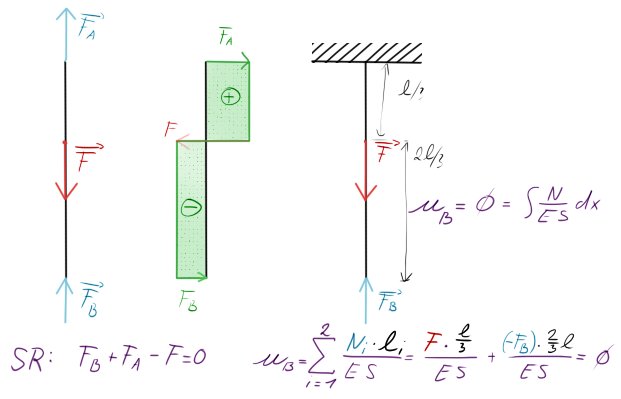
Pokud si vezmeme prut uvedený nahoře a nakreslíme si v úplném uvolnění směry sil, které předpokládáme a částečně uvolníme kvůli 1-násobné statické neurčitosti, příklad se bude vyvíjet takto:
Čeho si zde všimnout?
- Síla $F_B$ působí směrem nahoru. Proč? Protože pokud bude síla $F$ působit dolů, $F_A$ v reakci bude působit nahoru (kvůli natahování prutu) a dole se bude prut stlačovat, neboli bude reakční síla $F_B$ působit směrem proti stlačování.
- Jakmile jsem provedl ČU, napsal jsem DP $u_B = 0$.
- Úlohu můžeme řešit jak Castiglianem (zde nezobrazeno) (doplnit), tak i onou jednodušší metodou (zde zobrazeno).
Z DP jsme schopni dostat reakční sílu $F_B$, kterou, když dosadíme do rovnice SR, vyjde nám síla $F_A$ a úloha je vyřešena.
Pružná vazba
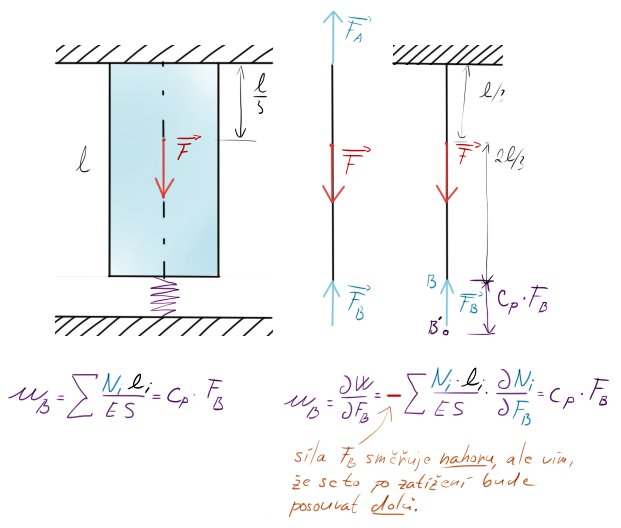
Jak si představit pružnou vazbu? Mno, logicky, buď tam bude pružina, nebo (už méně logicky) můžeme pružinu nahradit třeba koncem vetknutého prutu, který svírá s naším prutem 90°. Proto pokud hlavní prut zatížíme, začne se druhý prut „houpat“ a imituje pružinu.
Pružnost pružiny se určuje 2 parametry, těmi jsou poddajnost $[mm/N]$ a tuhost $[N/mm]$
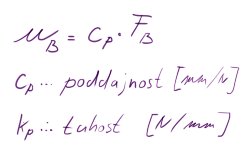
Maximální posun v bodě B $u_B$ je násobkem síly působící v bodě B $F_B$ a poddajnosti pružiny $c_p$.
Prut s pružinou, rovnou i úplným a částečným uvolněním + deformačními podmínkami by vypadal takto:
Dá se říct, že pružinu řešíme stejně, jako vetknutí, akorát musíme dbát na 2 věci:
- posuv $u$ bodu $B$ už není nulový, ale je závislý na tuhosti / poddajnosti pružiny … $c_p \cdot F$ nebo $F / k_p$
- pokud se nám pružina stlačí proti ose $y$, ale sílu máme zobrazenou po směru osy $y$, musíme do rovnice vložit mínus
Vliv výrobních tolerancí a změn teploty
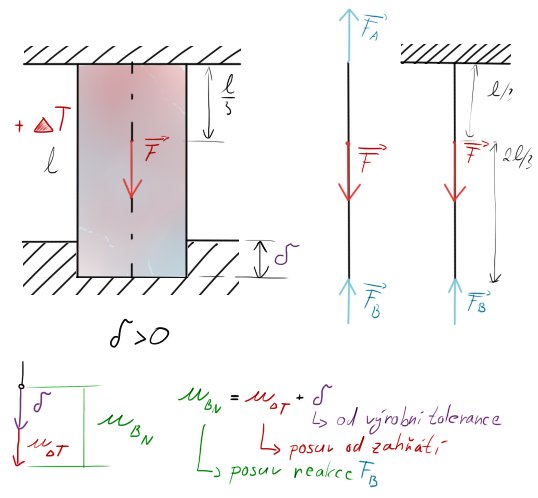
• Přesah $\delta$
$$u_{B_N} = u_{B_F} + u_{B_{F_B}}$$
Teplo roztahuje a mráz smršťuje, proto vždy budete vědět, kterým směrem bude působit posuv od teploty. Jestliže materiál podmrazíme -300°C, smrští se. Pokud (jako zde) bude zahřátý, prodlouží se o koeficient teploty.
Vzoreček pro tuto teplotní vlastnost je $u_{\Delta T} = \alpha \cdot \Delta T \cdot l$, neboli závislost změny teploty$\Delta T$, délky prutu $l$ a koeficientu alfa $\alpha$, který se (pokud se nemýlím) pohybuje kolem 1,2-1,4.
• Vůle ~nepodmíněně funkční vazba (vůle bude vždy vymezena)
Platí pro
$$\delta < 0$$
Nebo také již zmíněné ochlazení a „scvrknutí“ prutu.
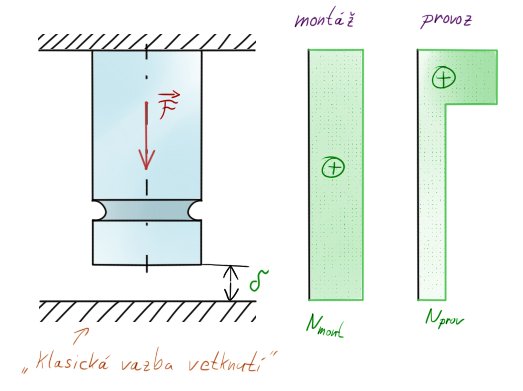
Jaký je rozdíl mezi montáží a provozem? Je velmi důležité kontrolovat oba stavy!
- Montáž ~ vlepíme hrazdu mezi dveře, utáhneme ji (hrazda drží tlakem na rám dveří v ose). Napětí je rovnoměrně rozprostřeno.
- Provoz ~ Poté v jednom místě začneme záporně tlačit osovým směrem. Je tedy vcelku logické, že jedna strana bude přetěžovaná a druhá naopak. Při opravdu velké síle se nám napětí na jednom konci vyrovná nule a my bychom byli schopni hrazdu sundat.
Vůle – podmíněně funkční (podmíněně SN)
Česky řečeno: nejsme si jisti, zda bude těleso staticky určité nebo neurčité, nevíme, zda se vůle vymezí. Máme tedy na výběr, jak už to tak často bývá, 2 možnosti řešení.
Optimistický přístup
Nebereme v potaz vazbu $B$ a vyřkneme, že je úloha staticky určitá. Počítáme s tím, řešíme rovnice a radujeme se, jak je to snadné. Na konci však musíme zkontrolovat, zda není posuv větší, než vymezená vůle. Pokud je menší, řešili jsme dobře. Pokud je větší, musíme jet od začátku tentokráte pro úlohu staticky neurčitou…
Pesimistický přístup (můj favorit)
Bereme v potaz vazbu $B$ a vyřkneme, že je úloha 1x staticky neurčitá (jak už jsme řešili několikrát v předchozích odstavcích). Zkoumám pak ale sílu $F_B$.
Pokud $F_B$ vyjde jako síla:
$F_B > 0$ … uhádli jsme směr (tlaková) a pesimistický přístup se nám vyplatil. Jestliže síla tlačí, znamená to, že vůle byla vymezena a počítali jsme dobře.
$F_B < 0$ … vůle vymezena nebyla, prut se druhého konce nedotkne a nám jen stačí rovnice přepočítat ještě jednou, tentokrát s touto silou nulovou, protože tam vlastně nic nepůsobí 😉
Proč mám pesimistický přístup radši? Protože když nám to nevyjde, nemusíme počítat nanovo. Rovnice už máme, jen si je zjednodušíme tím, že tam místo jedné neznámé přibude nula.
Pro dnešek snad bohatě stačí, příště nás čekají soustavy těles. No, příště… Za 12 hodin je přednáška :-p
Mmj pokud jsem byl dnes méně jasně informativní, mluví ze mě únava. Pokud je něco nejasného, odpovím rád do komentářů pod textem. Určitě to pomůže i některým lidem, kteří můžou mít stejné otázky.

One response to “PPI – 08 – staticky neurčité úlohy”