Pěknou středu přeji. Dnešní povídání bude značně kratší na text, bohatší na obrázky. Co nás čeká? Napřed lehké opakování předchozího, neboli kvadratické momenty a jejich algoritmus řešení, poté se podíváme na Vnitřní Výsledné Účinky schované v prutech. Prozatím nás toho moc nečeká, pouze pár příkladů a rozdělení na prosté namáhání. Podrobně se tím budeme zabývat příště.

Také bych rád oslovil ty z vás, kteří tyto postupy čtou, možná se stane, že tu na nějaké úterý / čtvrtek nebudu potřeboval bych přednášku nahrát. Sám na to používám Xperii Mini Pro (s aplikací Easy Voice Recorder Free), jak vidíte nic úžasného, jen je potřeba, aby kolem mobilu neseděly rušivé elementy. Tímto se vás ptám, pokud by bylo třeba, našel by se zde někdo, kdo by to za mě v mé nepřítomnosti byl schopen nahrát a poté poslat?

Pustíme se tedy do dnešní látky.

Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [5] – 19.2.2013 – Fuis: >> [MP3] <<

Opakování

Algoritmus řešení výpočtu a zobrazení kvadratických momentů

1. Rozklad na podoblasti
2. Jejich těžiště
3. Poloha těžiště celku
4. Kvdr. M. k osám těžiště podoblastí
5. Kvdr. M. k osám centrálním
6. Poloha hlavních os
7. Hlavní Centrální kvdr. momenty

Poslední 2 body (6. 7.) můžeme zkontrolovat díky Mohrovi. Nebojte, uvedeme si příklady krok za krokem.

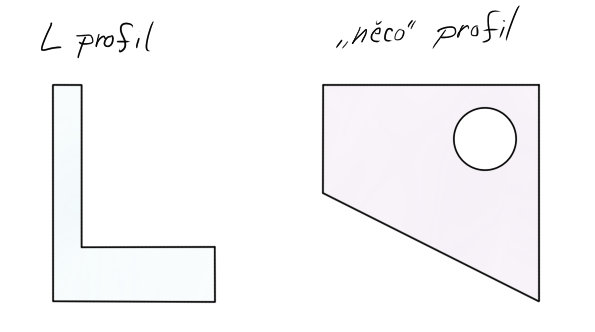
0) Řešené profily

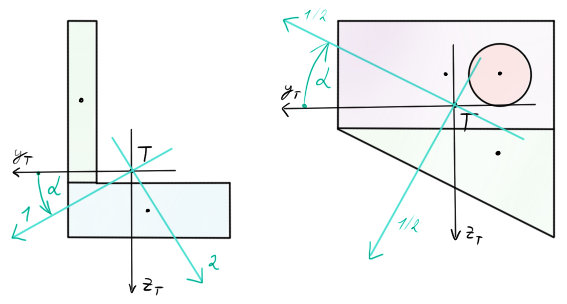
Pro tuto problematiku jsem si zvolil dva. L profil je vcelku lehká záležitost, „něco“ profil (dále jen X profil) je výsledkem sčítání a odčítání, ale algoritmus stále platí stejný.

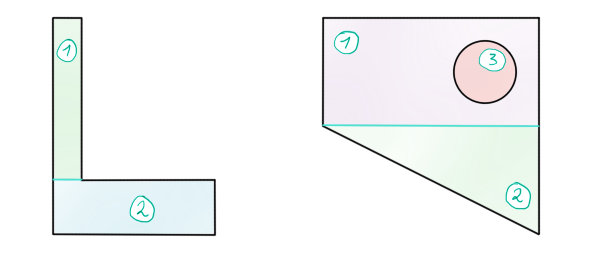
1) Rozklad na podoblasti

• L profil můžeme rozdělit jak se nám zlíbí. Nejvíce se vybízejí 2 rozdělení. Buď to seknu dole vodorovně, nebo svisle. Sekněme to tedy vodorovně.

• X profil musíme rozseknout na více podoblastí. Je jimi obdélník (1), trojúhelník (2) a díra – kruh (3).

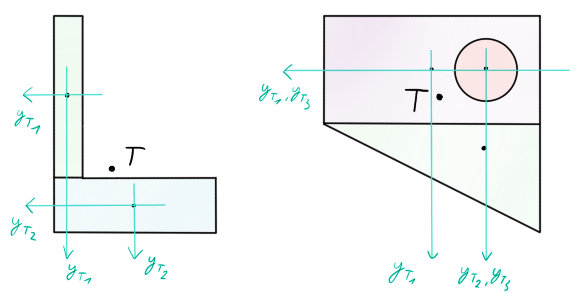
2) Najít těžiště podoblastí

• L profil má těžiště vždy uprostřed podoblastí, jsou tedy snadno najitelné. $T_1$, $T_2$

• X profil je ještě také vcelku jednoduchý. $T_1$, $T_3$ uprostřed, $T_2$ ve 2/3 zleva a zdola.

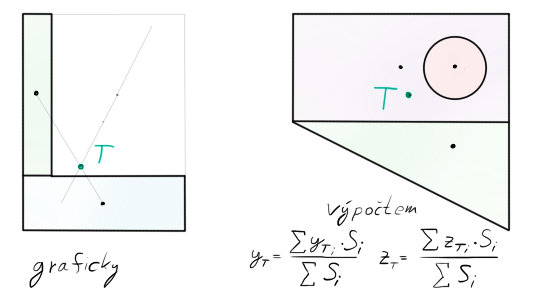
3) Najít polohu těžiště celého tělesa

• L profil ~ zde jsem zvolil grafickou metodu, kterou se ale podrobněji nebudu zabývat

• X profil ~ zde by se těžiště vypočetlo pomocí níže napsaných vzorců. Je to spolehlivá metoda pro homogenní (stejné materiálové rozložení v celém profilu – žádné přídavky např. dřeva, vduchové bubliny, jinak rozložený podíl grafitu, … Snad chápete) materiál. V okamžiku, kdy by se těleso skládalo z podoblastí/podtěles o jiných hustotách, musí se použít hmotnostní rovnice. Toto si kdyžtak někde najděte

4) Kvdr. momenty k osám těžiště podoblastí

• L profil čítá dva obdélníky. Použiji tedy vzorce $J_{y_{T}}$ a $J_{z_{T}}$ pro obdélník v těžišti, což je $bh^{3}/12$ a $b^{3}h/12$.

• X profil čítá obdélník, trojúhelník a kruh. Pro všechny vypočtu $J_{y_{T}}$, $J_{z_{T}}$, popř. $J_{yz}$ (trojúhelník). $J_{yz}$ bude pro kruh a obdélník nulový, protože osy profil půlí symetricky. A ještě $J_p$.

5) Kvdr. momenty k centrálním osám (osám procházející celkovým těžištěm)

• L profil ~ použiji Steinerovy věty. Ty mi poví: kvdr. momenty z těžišť podoblastí přesunu do jednoho bodu, a to („náhoda“) do těžiště celé soustavy. Z toho mi vzniknou dva $J’_{y_{T}}$ a $J’_{z_{T}}$ kvdr. momenty, které poté (díky větám minulým) sečtu a dostanu celkový $J_{y_{T}}$ a $J_{z_{T}}$ pro polohu v celkovém těžišti $T$.

• X profil ~ bude to prakticky stejné. Použiji opět Steinerovy věty, abych kvdr. momenty z těžišť podoblastí přesunul do jediného bodu, kde je poté sečtu. Bod jsem si vybral opět jako těžiště celku – $T$, protože je to prostě nejvýhodnější.

ALE protože kruh je díra!!! (jak je uvedeno na začátku (vybarvené to je jen kvůli tomu, že to považuji za podoblast)), musím kvdr. momenty této díry -odečíst- od momentů obdélníku a trojúhelníku, neboli: $J_{y_{T}} = J_{y_{T_{1}}} + J_{y_{T_{2}}} – J_{y_{T_{3}}}$ Pozor na to!

6) Určíme polohu hlavních os

Zde se jedná u obou profilů o naprosto totožnou věc. Použijeme rovnici pro zjištění úhlu Alfa hlavního $\alpha_h$, neboli:

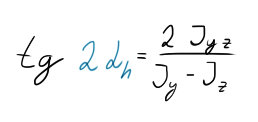Je vcelku poetické, jak moc mají lidi problém se v tomto vzorci dostat k $\alpha_h$. Jednoduše! Celou rovnici vydělíme $\tan$ a poté dvojkou. Zbyde nám tedy:

$$\alpha_h = \frac{1}{2} \tan^{-1} \left( \frac{2 \ J_{yz}}{J_y – J_z} \right)$$

Co to je ale to $\tan^{-1} x$… Arcustangens. Popř. se to dá napsat jako $1/\tan x$. Pro vypočtení Alfy tedy buď stiskněte na kalkulačce symbol $\tan^{-1}$, nebo napište $1/\tan (…)$ a čeho. Možná se smějete, proč to tu tak vysvětluji, ale opravdu byste se divili, kolik lidí má s tímto vzorcem problém 😉

Aplikujeme tedy rovnici a naznačíme otočení SS. Dostali jsme tedy Hlavní Centrální Souřadný Systém, neboli HCSS.

7) Kvadratické momenty HCSS

Co že to ještě jednou tedy vlastně je? Pokud budeme různě točit s osou $y$ a $z$, budou se nám měnit velikosti kvadratických momentů. Pokud však najdeme HCSS, deviační moment $J_{yz}$ bude nulový, neboli budeme v tomto pootočení znát jen a pouze $J_y$ a $J_z$, které budou nabývat maximálních a minimálních hodnot. Pojmenujeme je tedy $J_1$ a $J_2$. Už tedy nadále nebudeme počítat s nejistými „na úhlu natočení závislými“ proměnlivými kvdr. momenty, ale budeme mít pouze 2 čísla: $J_1$ a $J_2$.

Zjistím výpočtem díky rovnici:

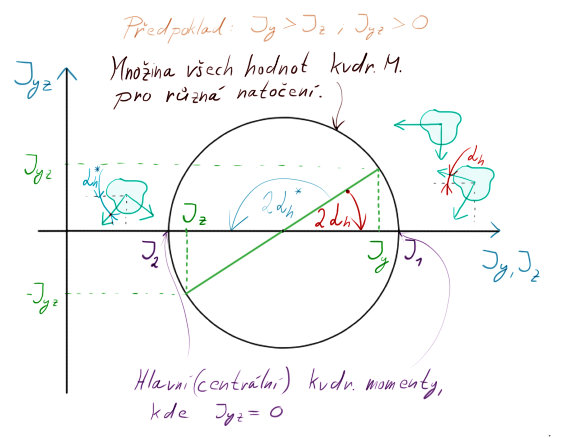
která vyplývá z nákresu v Mohrově rovině. Tam můžeme tyto systémy zakreslit. Postup je následující:

1. Osa horizontální $J_y$, $J_z$ a osa vertikální $J_{yz}$
2. Vynesení hodnot $J_y$, $J_z$
3. Vynesení hodnoty $J_{yz}$ v kladném směru
4. Průsečík $J_y$ a $J_{yz}$ nám dá bod. Zrcadlově ho můžeme spojit se středem (mezi $J_y$ a $J_z$)
5. Nakreslíme kružnici se středem v bodě $S$ (mezi $J_y$ a $J_z$) a poloměrem průsečíku $J_y$ a $J_{yz}$
6. Body, jež nám vznikly na ose $J_y$, $J_z$ jsou (zprava od největšího) Hlavní osové kvdr. momenty $J_1$ a $J_2$.
7. Úhel mezi $|S J_1|$ a $|S J_y \cap J_{yz}|$ je dvojnásobek Alfy hlavní ( $2\alpha_h$ )

 

Pro jistotu zde dávám ještě jednou z minulé lekce obrázek Mohrovy kružnice v Mohrově rovině pro kvadratické momenty.

To by bylo s opakováním vše, vrhneme se na VVÚ

Vnitřní Výsledné Účinky, alias VVÚ

Pokud máme kouli, kterou se v ruce budeme pokoušet rozdrtit, působíme na ni od našich hnátů vnějšími silami. Pokud bychom si ale v tom samém okamžiku zmrazili čas a kouli rozřízli a mohli nějakým způsobem vidět napětí, zjistili bychom, že i v té kouli (v onom materiálu uvnitř) působí nějaké ty síly na všechny strany (přiblíženo v první lekci), které tvoří napětí, nejspíš i deformace a další věci.

VVÚ jsou právě tyto síly. Síly, které nevidíme, ale můžeme je určit díky silovým zatížením vnějším, nebo třeba i gravitací, změně teploty a dalším vnějším vlivům.

Tak jako kvadratické momenty měly nějaké základní tvary (obdélník, čtverec, kruh, trojúhelník), VVÚ na tom není jinak. Budeme tedy určovat:

• Uzavřený zakřivený / zalomený prut
• Přímý prut staticky neurčitý
• Zalomený prut

Pozn: Fuis to rozdělil takto (výše), ale abych pravdu řekl, nejsem si jist proč. Moje rozdělení by nejspíše vypadalo:

• Přímý prut (rovná věc)
• Zalomený prut (rovná věc, kterou někdo násilně v jednom místě zvohl)
• Zakřivený prut (krásné hladké zakřivení, kružnice, oblouk)
• Pruty staticky neurčité (když je to chycené na více místech, než by „stačilo“)
• Uzavřený zakřivený / zalomený prut

Ale protože se řídíme (alespoň prozatím) Fuisovými přednáškami, nebudu mu do toho zasahovat.

a) Uzavřený zakřivený / zalomený prut

Pokud máme prut, jako je na obrázku dole, říkáme o něm, že je uzavřený a dle prostoru (2D / 3D) říkáme, že je buď 3x (2D) nebo 6x (3D) staticky neurčitý.

Pokud tento prut říznu jednou, z uzavřeného se stane otevřený prut.

Pokud ten samý prut říznu podruhé, neboli od uvolněného prvku, mohu určovat jednotlivé VVÚ, při tom však vzniknou další 3 neznámé.

Jak už bylo řečeno někdy minule, čím více staticky neurčitá úloha je, tím je to lepší z hlediska tuhosti, protože se nám rozloží napětí souměrněji. Za cenu pár neznámých, které můžeme určit např. díky Castiglianově větě.

b) Přímý prut staticky neurčitý

Můžeme si zde uvést příklad:

Zde vidíme, že počet možných podmínek (pro 2D: 3) nedostačuje počtu neznámých (4 = $F_A$, $F_B$, $F_{C_y}$, $F_{C_x}$), statická neurčitost je tedy $S=1$. V tomto případě můžeme odhadnout, že $F_{C_x}=0$, protože žádná jiná x-ová síla zde nepůsobí (pokud by se síla $F$ nahla, už je průser), nemusíme tedy používat Castiglianovu větu.

VVÚ zde je jen odhadnuté. V příštích týdnech si povíme, jak to pro jednoznačné místo spočítat přesně.

c) Zalomený prut

Jaké jsou problémy zalomeného prutu? Jestli tam vůbec nějaké jsou

Jsou… A to je právě ono zalomení. Pokud totiž v tomto místě vyjde největší napjatost, nemůžeme ho „tak docela„ brát v úvahu. V tomto zlomení totiž nejsou splněny prutové předpoklady, blíže předpoklad: „průřez je spojitý, souvislý“. Je tam lom.

Řeší se to zavařením onoho místa zlomu, tím prutu dodám materiál, zvýším mu tuhost a střednice se jakoby zaoblí, takže mohu místo uvažovat jako „prut“.

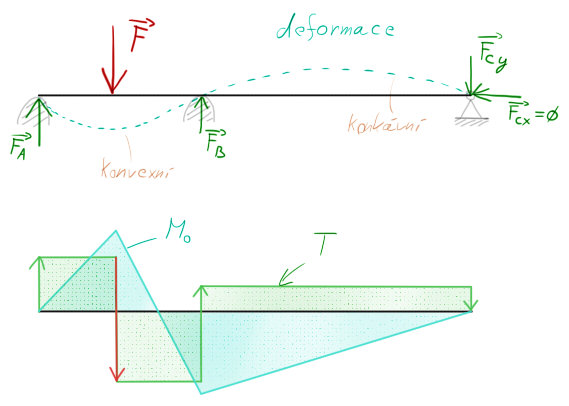
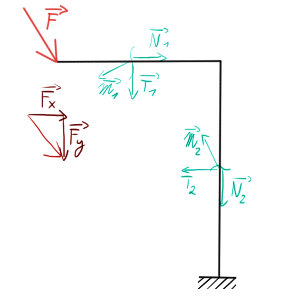
Příklad zalomeného prutu zatíženého šikmou silou tak, že vyvolává jak $T$, $N$, tak i $M_o$.

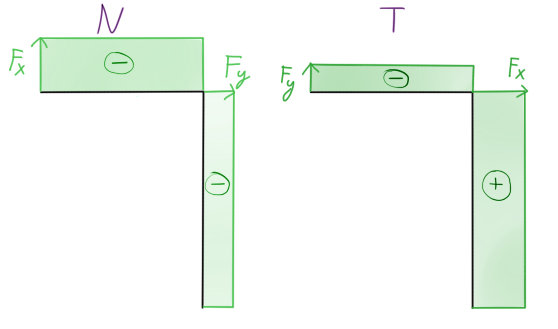
Zde jsou vyřešeny (odhadem) posouvající síly $N$ a $T$:

A zde je (odhadem) vyřešen moment. Bohužel však nevíme, jakým směrem síly působí, proto jsem zde vyřešil všechny tři případy.

• Síla by svou nositelkou prut neprotnula – modrá barva

• Síla by svou nositelkou protnula prut přesně v místě vetknutí – červená barva

• Síla by svou nositelkou protnula prut někde nad vetknutím – fialová barva

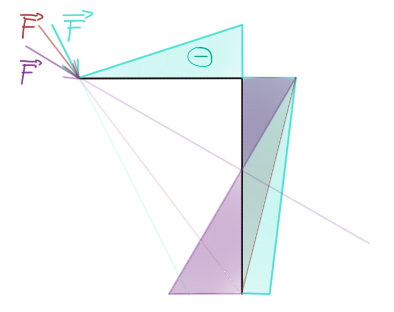Všimněte si dvou věcí. 1) Jestliže se jedná o sílu $F$, která protíná prut ve vetknutí, moment je zde nulový. 2) V místě zakřivení se velikost momentu jakoby „překlopí“ na druhou část prutu. Je tam stejná velikost. Platí vždy, pokud v onom místě nepůsobí přídavný moment.

Rozdělení namáhání

V Pružnosti Pevnosti I se budeme zabývat pouze:

1. prostým tahem / prostým tlakem (a následnou možnou ztrátou stability)
2. prostým krutem
3. prostým ohybem
4. smykem (prostý smyk neexistuje, vždy ještě vyvolá nějaký moment)

V Pružnosti Pevnosti II se poté budeme zabývat:

1. Kombinovaným namáháním, což je krut + smyk, tah/tlak + ohyb, nebo všechny tři, atd.
2. Neprutovými tělesy (disk, deska, momentová/bezmomentová skořepina)
3. Trhlinami v tělesech
4. Únavou z namáhání

Prosté namáhání:

Napjatost a deformaci lze řešit odděleně.
Lze uvolňovat prvek konečných rozměrů v nedeformovaném stavu.

Neprosté namáhání:

Napjatost a deformaci nelze řešit odděleně.
Uvolňujeme v deformovaném stavu.

---

 

Tímto pro dnešek skončíme. Audio soubor obsahuje ještě nějakých 20 minut povídání o prostém tahu / tlaku, ale to si necháme až na celkové vysvětlení do příštího článku.