A máme zde další přednášku 🙂 Poněkud později, než je obvyklé, čtenářům se tedy omlouvám. Byla tu taková věc okolo přehnaně moc věcí, které jsem musel za krátký časový úsek zvládnout, a to mi ještě některé pendují…
A máme zde další přednášku 🙂 Poněkud později, než je obvyklé, čtenářům se tedy omlouvám. Byla tu taková věc okolo přehnaně moc věcí, které jsem musel za krátký časový úsek zvládnout, a to mi ještě některé pendují…
Dnes budem pokračovat s vysvětlováním tahu/tlaku a jeho odchylek, neboli vrubů, zápichů a dalších tvarových nerovností.
Mám také o 3 pluginy více ^_^ Tak je vyzkouším použít, mělo by to opět přidat na nějaké té přehlednosti a usnadnění pochopení 🙂
Obsah článku
Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [7] – 26.2.2013 – Fuis: >> [MP3] <<
Odchylky
Jestliže se bavíme o prostém tahu/tlaku, nemusí to být někdy tak medové, jak to na první pohled může vypadat. Vyskytují se např. nějaké tvarové nerovnosti, nebo odklonění od přímosti, přidáme doprostřed sílu, budem počítat s gravitací, zkusíme to kroutit, nebo tam uděláme díru. 🙂
Co však v těchto případech? Vykašlat se na to? Nn 🙂 Je to lehčí, než se zdá.
Odchylka od přímosti
Pokud bych měl například vetknutý nosník, který by byl ale malinko zakřkřivený, přesto bych však tahal silou kolmou k průřezu na jeho konci, tvořil by se po jeho průběhu moment (o velikosti $F \cdot r$). A tam, kde se tvoří moment, je i nějaká smyková síla.
Nemusím asi dál říkat, že tam, kde je jak normálová, tak i smyková síla a ještě k tomu moment už asi prostý tah/tlak nebude platit.
S jedinou výjimkou
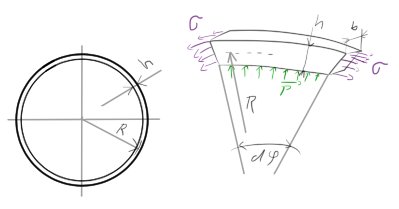
A to pokud se jedná o tenký kruhový prut, který je zatížen rotačně symetricky. Jak si takovou větu představit v praxi?
Zde máme zobrazen onen kruhový prut, který je zatížen rotačně symetricky (třeba plyn v trubce). Dále to už ale nebudu rozebírat.
Nekonstantní normálová síla N
Co si pod tímto pojmem představit?
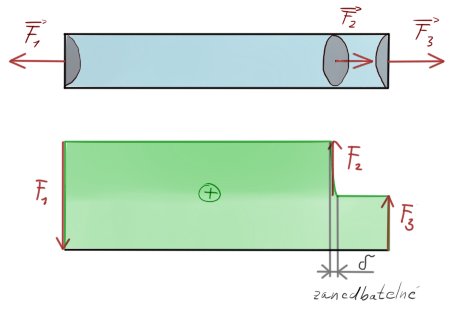
Vezmeme-li v úvahu, že na prut nemusí ve směru jeho střednice a v těžišti působit jen jedna síla, ale můžou být dvě, nebo můžeme počítat s jeho hmotností ve svislém zavěšení, jsou tu 2 možné případy, které bychom měli znát a probrat, protože jsou naprosto nejčastějšími odchylkami, když se počítají příklady na zápočet / zkoušku, tak i v reálném životě. (I když tam je prostý tah/tlak veeeeelmi těžké zařídit).
Spojitá změna
Spojitá, nebo také plynulá změna zatížení. Máme zde zatížení z již už zmíněné gravitace $\vec{g}$. Vetknutý nosník zavěsíme svisle na stěnu a necháme viset. Pokud by to byl kilometrový prut, nejspíš by se i o pár centimetrů rád posunul. Uvažujme však reálně a uveďme si příklad:
Zde sledujeme, že normálová složka VVÚ se zvětšuje v závislosti na délce prutu. Její velikost $N$ pak vychází ze vzdálenosti a síly gravitační složené z hmotnosti $m$ vynásobené gravitační konstantou $g$ a hmotnost závisí na objemu $V$ a hustotě $\rho$. V komplikovaném tělese by nebyla normálová složka VVÚ takto krásná, ale i tak by měla být „vcelku“ plynulá.
Skoková změna
Ono se řekne „skoková“, ale v reálu je změna také spojitá. Avšak minimálně, proto můžeme říci, že je tam jakýsi náhlý skok.
Toto zatížení se může uskutečnit třeba tím, že uchytíme těleso někde kolem poloviny do kleští a začneme tahat / tlačit. Nebo (lepší případ) by se kolem jeho obvodu obepnula nějaká objímka, která by ho táhla značně pravidelněji, aby byla silová výslednice v těžišti průřezu.
Proměnnost průřezu – neprizmatického
Zatím jsme uvažovali změnu silovou. Co když ale budeme mít změnu tvarovou. Například v důsledku zvýšené teploty, či jiného důvodu, by se prut lehce „nafoukl“. Prutové předpoklady nám říkají, že aby platil prostý tah/tlak, musí být prut přímý, prizmatický a homogenní. Pokud druhou podmínku nedodržíme, můžou opět nastat 2 příklady:
Spojitá změna
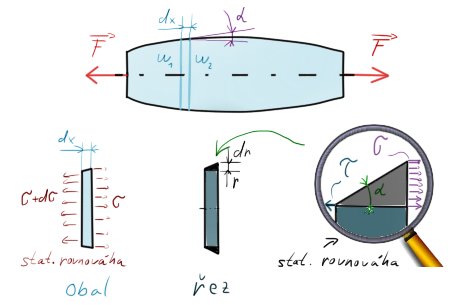
Nejprve si ukážeme, jak taková spojitá změna vypadá u onoho „nafouklého“ prutu:
Zde vidíme, že je to jakési lehké odklonění. Z obrázku také vyplývá pár věcí:
- Pokud uděláme řez a zahrneme statickou rovnováhu, vyjde nám, že aby platila stejná síla jak na větší ploše, tak na menší, napětí na menší musí obsahovat ještě určitý přírůstek $d\sigma$.
- Jestliže uděláme průřez a zaměříme se jen na vrchní část (v lupě detailněji), zjistíme, že při stejné statické rovnováze máme nějaké působící napětí $\sigma$ směrem doprava a „nic“ doleva. Je tedy jasné, že tam musí působit „nějaké“ napětí, a to v tomto případě smykové $\tau$.
Dále to nebudu rozpitvávat, nevzpomínám si, že bychom tento typ úlohy někdy v PPI dělali.
Skoková změna
VELMI častá změna prizmaticity prutu. Leckdo ji zná pod pojmem zápich či osazení.
Zápichy jsou většinou chtěné tvarové změny, které chceme ve výsledném produktu mít, aby plnily funkční požadavky výrobku (aby se to dalo uchytit).
Někdy se však stane, že jsou i nefunkční. To nastává mnohdy kvůli nějakému úžasnému designerskému nápadu, který je žádoucí z hlediska zákazníka, protože pak cílený produkt vypadá lépe, avšak nežádoucí z hlediska výpočtářského, protože nám značně zkomplikuje život. Prodávat se však musí 🙂
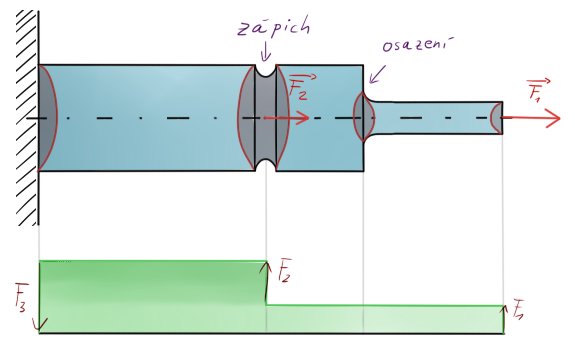
Saint-Venant! ~ V červených oblastech neplatí prutové předpoklady a výsledné napětí je tam tedy komplikovanější.
Zde máme zatížený nosník 2 silami. $F_1$ a $F_2$. Na dvou místech prut není prizmatický – obsahuje jedno osazení a jeden zápich. Saint-Venant nás upozorňuje na možná červené místa, kde nejsou splněny prutové předpoklady, proto pozor.
Něco se však už za ta léta naštěstí pořešilo a díky mnohaletým pokusům, zničeným výrobkům a statistikám byla naše starší generace a subgenerace schopna stvořit tzv nomogramy, které mají 3 parametry.
Podíl průměrů $r/d$ a $D/d$ a jako třetí parametr $\alpha$, který se z nich (nomogramů – grafů) právě snažíme vyčíst.
Jestliže poté určujeme napětí v místě onoho neprizmatického místa zápichu či osazení, nejprve vypočteme napětí bez vlivu této tvarové změny, a poté ho vynásobíme koeficientem $\alpha$.
Ten zjistíme právě díky nomogramům (v praxi), nebo jej učitel na písemce/zkoušce zadá.
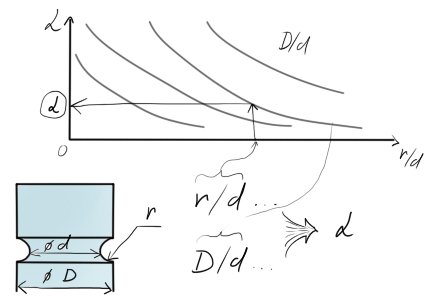
1) Máme vhodný nomogram. 2) Spočtem podíly $D/d$, $r/d$ -> vyjdou nám čísla. 3) Ty vyneseme na osu. 4) Protne se nám v jednom místě křivk s $r/d$ veličinou. 5) Odečteme z toho koeficient $\alpha$
$\alpha$ se pohybuje v rozmezí:
1 .. 3 – velké poloměry
3 .. x – malé poloměry
Z čehož můžeme vyčíst, že čím menší je poloměr zápichu / osazení, tím nebezpečnější se místo stává z hlediska napětí.
Testový ukázkový příklad
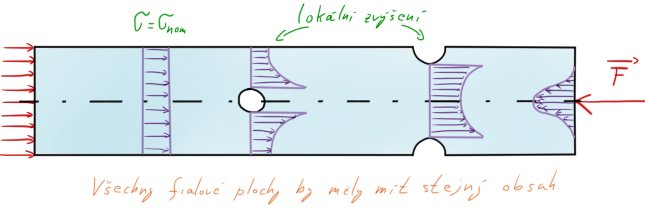
Zde vidíme zkouškový teoretický příklad. Prut je zatížen zleva tlakem $p$, zprava silou $F$. Obě jsou ve statické rovnováze (SR).
Pokud sledujeme napětí uvnitř prutu,
- 1. místo ~ napětí nominální $\sigma_{nom}$ je rovno napětí tlakovému $\sigma$ působícího zleva.
- 2. místo ~ díra deformuje napětí, které bude mít největší hodnotu okolo díry a bude náležitě klesat až k okraji, kde bude jeho hodnota menší než u napětí $\sigma_{nom}$ na okraji prutu.
- 3. místo ~ zápich deformuje napětí tak, že uprostřed prutu je nejmenší (menší, než nominální) a v působišti zápichu největší.
- 4. místo ~ síla $F$ způsobuje největší nárůst napětí v místě působiště a rapidně se zmenšuje a rozprostírá do blízkého působiště, kdy u okrajů je téměř nulové.
U zkoušky se snažíme, aby měly všechny fialové oblasti –stejný obsah– na první pohled (což je mi z hlediska síla / díra moc nepovedlo 🙂 ), tak pozor na to. Nejlépe tam toto vysvětlení připsat.
Šroubovitost prutu
K ní jen malinko. Pokud mám prut, kterým kroutíme a je kruhového či čtvercového průřezu, nemá pak míra krutu (šroubovitost) žádný vliv na hodnoty prostého tahu/tlaku.
Ovšem v případě obdélníkového / trojúhelníkového či I, L průřezu je to úplně jiná věc 🙂 Natáčení HC osy průřezu po délce prutu vyvolává vznik smykových napětí, takže nám opět nesplňují prutové předpoklady pro prostý tah/tlak.
To je pro dnešek vše, příště se koukneme na krásné a komplikované téma staticky neurčitých úloh. Protože prakticky vše máme staticky neurčité. Už nejsme ve statice 🙂