 Druhý týden nám završil a konečně jsme probrali něco, co jsme probrané už měli mít tak ve 2. 3. hodině. Ale zas ne 1., jak minulý rok na cvičení 🙂
Druhý týden nám završil a konečně jsme probrali něco, co jsme probrané už měli mít tak ve 2. 3. hodině. Ale zas ne 1., jak minulý rok na cvičení 🙂
Dnes nás tedy čeká seznámení s kvadratickými [kvdr] momenty (ta zkratka je má osobní, nevím, zda to tak někdo zkracuje…) a to nějaké ty pravidla, která pak můžeme využít (reálně ani tak ne… vše se hledá v praxi v tabulkách) na výpočet kvdr. momentů složitějších těles, skládajících se z jednodušších těles – obdélník (čtverec), kruh a trojúhelník. Poté si řekneme něco k osám a jak je posunout či natočit, k čemu to natočení vůbec je (proč se s tím sr*t) a jak to udělat lépe, kvalitněji a přehledněji pomocí Mohrovy kružnice (roviny). Jde se do práce 🙂
Pozn. Trochu se mi tato lekce zdržela v publikování. Důvodem byla příprava na pohovor v zatím nejmenované firmě v nejmenovaném městě a 3-denní krásný výlet po horách s mou drahou polovičkou ^_^ Doporučuji, pročistí to nádherně hlavu.
Obsah článku
Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [4] – 14.2.2013 – Fuis: >> [MP3] <<
Kvadratické momenty
Čo to k sakru?
Půjdem na to od konce. Abyste pochopili nějaké souvislosti.
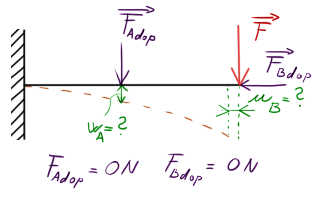
Zadání – máme vetknutý nosník, na něj působí síla (z minulé přednášky jen tak pro -představu-).
Myslíte, že se bude chovat naprosto stejně, ať už to bude z jakéhokoli materiálu či tvaru?
Pokud bude z hliníku, nejspíš vydrží méně, než když bude z oceli. To máme charakteristiky $E$ a $\mu$ (Poissonovu konstantu).
Ale co když bude kulatá. Ohne se více, než když bude čtvercová, popř. obdélníková, nebo to bude I profil, O profil či L profil, který může být natočený prakticky jakýmkoli směrem?
Můžeme se tedy shodnout, že je důležité jak profil vypadá.
Už teď prozradím, že profilů je velké množství. Mnoho z nich je však symetrických a mnoho z nich se dá zesnadnit pomocí jednoduchých profilů, které si dovedeme zapamatovat i zpaměti, je to:
• Obdélník
• Čtverec (speciální forma obdélníka, kdy $b = a$)
• Kruh (plný, či dutý)
• Trojúhelník (ve škole prakticky nebudem (nejspíš) na cvičeních používat)
Tyto profily se charakterizují kvdr. momenty, které si teď přiblížíme.
Jen taková poznámka: existují i Lineární (statické) momenty průřezu ($\Psi$), které značíme $U_y$ a $U_z$ (pokud je průřez kolmý na osu $x$), ty se používají hlavně pro polohu těžiště a tak. Nic, co by nás mělo extrémně zajímat.
Osové kvdr. momenty
$$J_y = \int_{\Psi} z^{2}dS$$
$$J_z = \int_{\Psi} y^{2}dS$$
Deviační kvdr. momenty
$$J_{yz} = \int_{\Psi} z \cdot y \ dS$$
Polární kvdr. momenty
$$J_{p} = \int_{\Psi} \rho^{2} dS$$
Kde $\rho$ je –vzdálenost k pólu-. (není to hustota)
Co nám z toho všeho plyne? Pokud budeme chtít vypočítat opravdu nějaké veeelmi komplikované tvary, toto jsou integrály, které použijeme. Je vhodné si uvědomit, že $J_{y} = z \cdot z$, $J_{z} = y \cdot y$ a $J_{yz} = z \cdot y$.
Polární kvdr. moment se pro $P \equiv O$ dá také napsat jako součet osových kvdr. momentů, neboli:
$$J_{p} = J_{z} + J_{y}$$
A další velmi důležitá věc, pokud pól náleží těžišti, $J_{p} = 0$.
Modul průřezu
Je jakási veličina, která dělí ony kvadratické momenty charakteristickým rozměrem (většinou).
V ohybu
$$W_{o} = \frac{J_{o}}{h_{o}}$$
kde $J_{o}$ je osový moment a $h_{o}$ je charakteristický rozměr (rozměr, který těleso nějakým způsobem charakterizuje, u kruhového průřezu je to poloměr, u čtvercového / obdélníkového je to jeho polovina přepony).
V krutu
$$W_{k} = \frac{J_{p}}{R}$$
kde $J_{p}$ je polární kvdr. moment a $R$ je vnější poloměr průřezu.
Dále platí různé zajímavé (usnadňující počítání) věty
Je dobré si je zapamatovat, protože jejich znalost se pak v písemce projeví tím, že na zadání mrknete a z voleje řeknete „tady bude $J_{p}$ nulovej a $J_{y}$ se bude rovnat $J_{z}$“, vyhnete se tak někdy naprosto zbytečnému počítání.
První věta
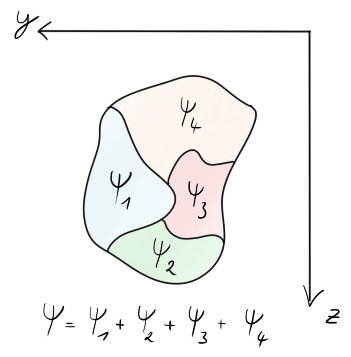
Kvdr. momenty celého průřezu k daným osám/pólům jsou rovny součtům kvdr. momentů částí průřezu k témže osám/pólům.
Česky řečeno: Součet oněch kvdr. momentů průřezů ($\Psi_{1} .. \Psi_{4}$) k ose $y-z$ je roven kvdr. momentu celého průřezu k té stejné $y-z$ ose.
 Druhá věta
Druhá věta
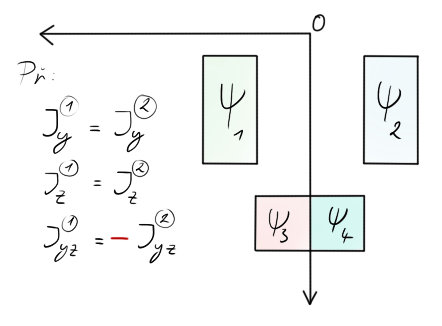
Osové kvdr. momenty symetrického průřezu k ose symetrie k ose k ní kolmé jsou stejné.
Česky řečeno: Pokud alespoň jedna z os bude symetricky půlit onu oblast/podoblast (průřez), můžeme napsat, že se její kvdr. momenty rovnají.
 Třetí věta
Třetí věta
Osové kvdr. momenty symetrického průřezu k ose symetrie a k ose k ní kolmé jsou rovny dvojnásobku osového kvadratického momentu jeho symetrické části ke stejným osám.
Česky řečeno: Prakticky to stejné, co věta nahoře. Poku si vezmeme (nahoře) průřez $\Psi_{3}$ a $\Psi_{4}$, stačí nám vypočíst jen $\Psi_{3}$, abychom věděli $\Psi_{4}$.
Čtvrtá věta
Deviační kvadratický moment symetrického průřezu k pravoúhlému souřadnému systému, kde je alespoň jedna z os osou symetrie, je roven 0.
Česky řečeno: Pokud máme průřez, kterej je osou alespoň v jednom směru nějakým způsobem řízlej (ať už kolmo nebo šikmo), deviační moment $J_{yz} = 0$.
Průřezy
Jak už jsem naznačil, velké, komplikované a hnusné profily se dají popsat jednoduchými profily. Pokud tedy nemáme strojnické tabulky, nebo zlého vyučujícího, musíme (dle věty nahoře) spojit několik jednoduchých profilů dohromady (všechny musí být napsané k jedné ose), aby nám vyšlo ono monstrum.
Pustíme se do nich.
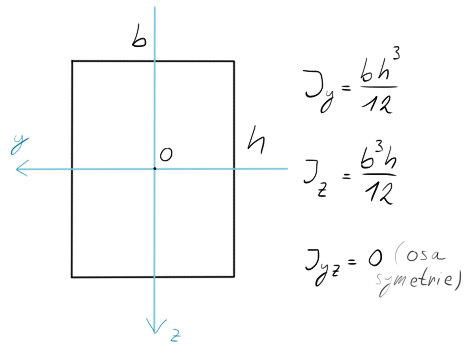
Obdélník
Pokud budeme počítat s centrálním systémem (jeho nulový bod bude ležet v těžišti tělesa), můžeme kvadratické momenty vypočíst dle integrálů uvedených výše, ale ve výsledku nám vyjde něco velmi lehkého, snadno zapamatovatelného (avšak lehce spletitelného 🙂 ).
Čtverec
Je to speciální případ obdélníka, kdy strana $b = h$. Je tedy logické, že bude mít prakticky stejné vzorce, jako obdélník nahoře.
Kruh
Ať už v PPI či PPII, s tímto tvarem se budete setkávat asi nejčastěji. (Krom výpočtů trhlin, kde to bude vždy nějaký obdélník či čtverec)
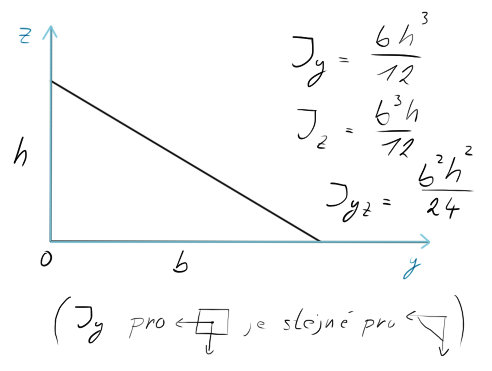
Trojúhleník
Z minulého roku si pamatuji, že jsme tento profil brali v první, možná druhé hodině, pak se (možná) vyskytl na prvním zápočtu a od té doby jsme o něm neslyšeli. Abych pravdu řekl, téměř jsem zapomněl, že něco podobného existuje. Ale co víte, tento rok se s ním počítat může 🙂
Zde si můžete všimnou, že $J_{y}$ pro čtverec, jehož nulový bod je v těžišti, je stejný jako $J_{y}$ pro bod trojúhelníku na jeho ostrém okraji. Z toho se můžeme „dovtípit“, že $J_{y}$ pro čtverec, jehož nulový bod v těžišti nebude, ale bude na ostrém okraji bude jiný než pro ono těžiště. Ale o tom později 🙂
Jak už jsem naznačil na začátku, probrali jsme všechny možné profily, ale nezmínil jsem se ještě, proč bychom měli posouvat či ohýbat osy.
Kvdr. momenty průřezu při transformaci souřadnic
Dělí se na:
• Posuvy
• Natočení
Posunutí
Posunutí. Proč bychom ho měli vyžadovat? Proč by nás mělo zajímat? Existují jakési Steinerovy věty, díky kterým jsme schopni posouvat souřadný systém z těžiště do jiných míst. Pokud (jak už bylo řečeno výše) máme nějaký průřez rozdělený na spoustu menších průřezů, přesně pro tento případ se posunutí hodí.
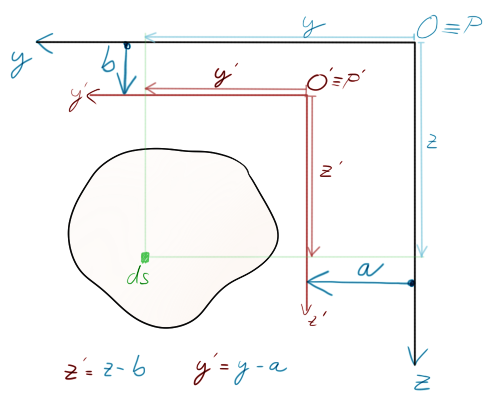
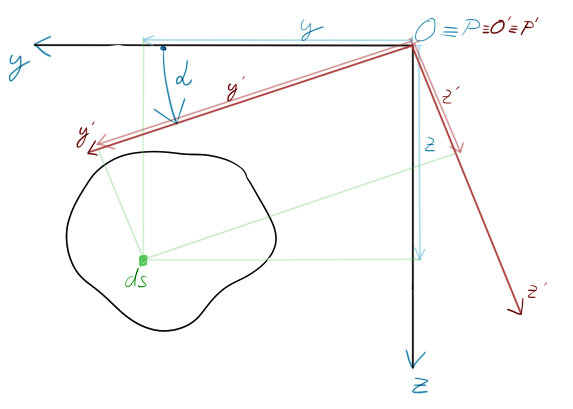
Graficky znázorněné ho máme zde:
Jak zde vidíme, že pokud chceme z bodu $O$ přemístit souřadný systém do $O^{\prime}$, vystačí nám jednoduché vzorečky. Pokud však nechceme přepočítávat opětovně kvdr. momenty k nové $O^{\prime} y^{\prime}-z^{\prime}$ ose, použijeme
Steinerovy věty:
Ty nám říkají, že pokud chceme posunout kvdr. moment $J_{y}$ z těžiště do jiné polohy, bude to tak, že k $J_{y_{T}}$ přičteme čtverec vzdálenosti kolmé na hledanou osu a vynásobíme to plochou řezu, ke kterému kvdr. moment počítáme.
Ještě jednou opakuji:
Steinerovy věty se používají, pokud chceme přenést kvdr. momenty z těžiště do nějakého jiného bodu (klidně i jiného těžiště).
V praxi to pak znamená, že řez, který si rozdělím na 3 podoblasti, spočtu tím, že z těžiště podoblastí přesunu všechny kvdr. momenty do těžiště kompletního řezu, sečtu je a mám výsledný kvdr. moment.
Pozor!
$J’_{y}$ i $J’_{z}$ nám vždy musí vyjít kladné, protože ať už posouváme přes $a$, $b$, či $-a$, $-b$, kvadrát nám to zkladní. Ovšem $J’_{yz}$ mezi sebou $a, b$ násobí, takže může vyjít záporný. Na druhou stranu pro kontrolu, pokud nám vyjdou $J_{y}$, $J_{z}$ záporné, někde bude chybka. 🙂
Info: V těžišti se nacházejí nejnižší kvadratické momenty. Pokud se od něj budeme vzdalovat, budou jejich velikosti jen narůstat.
Natočení
Natočení. Proč bychom ho měli vyžadovat? Proč by nás mělo zajímat? Steinerovy věty jsme použili pro posunutí Souřadného systému (dále jen SS) do centrální polohy, neboli se z něj stal CSS. My však budeme hledat tzv. hlavní CSS (HCSS). Co znamená slůvko hlavní?
Hlavní ~ deviační kvadratický moment je nulový. $J_{yz} = 0$.
Hledáme tedy takový úhel natočení, abychom se dostali do HCSS, kdy je $J_{yz} = 0$. Proč? Protože se nám extrémně zjednoduší pár různých výpočtů. Budeme moci počítat s hlavními napětími a hlavními kvdr. momenty. Hlavní je takové magické slůvko, které budeme mít rádi. ^_^
Grafické znázornění natočení by mohlo vypadat takto:
Hádám, že stále nechápete, proč to vůbec dělat. Snad se k tomu přiblížíme později při nějakých konkrétních příkladech. Pro teď jen řeknu, že nalezením tohoto úhlu, neboli nalezení HCSS máme jakýsi optimální souřadný systém, který je jakoby rovnovážný, nebo jak to nazvat, z hlediska zbytečného kroucení. Jestli vás matu, neberte tento odstavec vůbec v potaz.
Nalezení hlavního úhlu $\alpha$:
Přes velmi komplikované vzorce a cosiny a další zmetky se dostaneme k tomuto vzorci, který radím zapamatovat a uvědomit si, co tam jednotlivé části znamenají. Pro jistotu si je shrneme.
$J_{yz}$ … Deviační moment. Spočteme pomocí Steinerových vět, popř. vyčteme z tabulek / spočteme přes integrál.
$J_{y}$ … Kvadratický osový moment k ose y (Steiner / pro jednoduchá tělesa si pamatujeme.)
$J_{z}$ … ——————– || ——————— z (nápodobně, jsou to takové ty $bh^{3}/12$ atd)
$\alpha_{h}$ … Hlavní úhel natočení. Díky němu se dostaneme do hlavního souřadného systému.
Co se s takovým úhlem Alfa dá dělat? Může dosahovat hodnoty 0 – 360°? Jak vidíme z rovnice výše, je to jakási závislost (podíl) deviačního momentu ($J_{yz}$) na rozdílu momentů osových ($J_{y} – J_{z}$). Tuto závislost si můžeme vynést do Mohrovy roviny, díky níž si uděláme jakýsi pestřejší přehled o tom, jak to s tím natočením vypadá.
Mohrova rovina
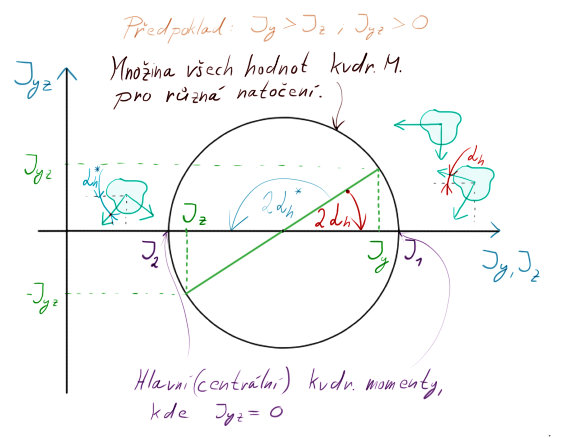
Mohrova rovina je grafické znázornění kvadratických momentů $J_{y}, J_{z}, J_{yz}$.
Nebudu dlouho zdržovat, zde je zobrazena. Přidal jsem tam polohy hlavních kvdr. momentů $J_{1}, J_{2}$ (řazeno vždy od největšího k nejmenšímu … 1 -> 2 -> 3 atd.), dále poznačil hledaný úhel (pozor, v mohrově rovině rovině je to (díky různým přepočtům) $2 \cdot \alpha$!), a tři nástřely otočení SS ve třech místech (ty divné modrozelené „buňky“).
Zde vidíme, že pro původní natočení, kdy existuje $J_{yz}$ máme vodorovnou a svislou osu $y-z$. Pokud však natočíme osy o $\alpha_{h}$, (bod $J_{1}$) nebo o $\alpha_{h}^{*}$ (bod $J_{2}$), deviační moment se nám vynuluje a $J_{y}$ se zvětší na $J_{1}$, resp. $J_{z}$ se zmenší na $J_{2}$.
Tato dvě hlavní kvadratická napětí se dají spočíst i početně:
Další ze vzorců, který si určitě pamatovat. 🙂
Zkoušková otázka
Na konec bych přidal jednu ze zkouškových otázek.
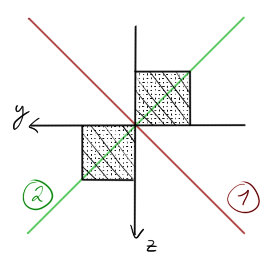
Otázka nejspíš bude znít: Která osa je 1 a která 2.
Pokud je $J_{yz} < 0$
Řešení jsem si už dovolil vyznačit. Osa 1 protíná 1, 3 kvadrant. Osa 2 protíná 2, 4 kvadrant.
Pokud je $J_{yz} > 0$
Pokud by to bylo opačně, Osa 1 by protínala 2, 4 kvadrant a osa 2 by protínala 1, 3 kvadrant.
Jak na to ale přijít?
Pokud! si to jde graficky představit, můžeme si říci:
Když začneme těleso rotovat kolem nějaké osy, kdy to bude klást větší odpor? Právě tam je hodnota kvadratického momentu větší a osu poznačíme číslem 1.
Pokud! je situace spekulativní, řídíme se hodnotou deviačního momentu.
$J_{yz}<0$
osa 1 … 1, 3 kvadrant
osa 2 … 2, 4 kvadrant
$J_{yz}>0$
osa 1 … 2, 4 kvadrant
osa 2 … 1, 3 kvadrant
To je pro dnešek vše, snad se líbilo. Příště si tuto látku v krátkosti zopakujeme a začneme VVÚ, alias Vnitřní Výsledné Účinky. Látku, na které pohoří významné procento lidí u PPI a nemilosrdně vyletí u zápočtu / zkoušky mnoho studentů v PPII.
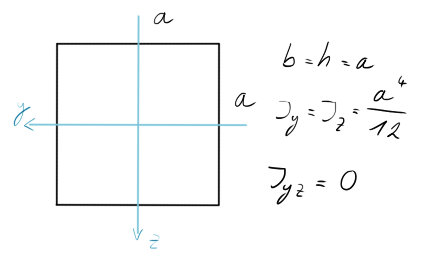
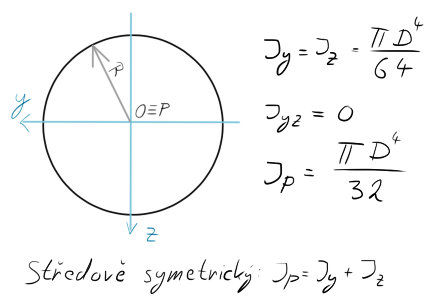
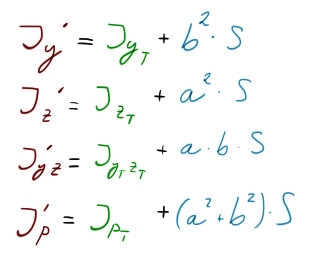
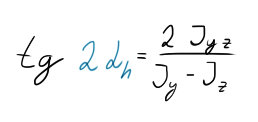


10 responses to “PPI – 04 – kvdr. momenty, Steinerovy věty posunutí, natočení a Mohr”