 Zdravím potenciální čitatele tohoto blogu. Rozhodl jsem se, alespoň prozatím (dokud mi do toho něco neskočí) navštěvovat přednášky pana docenta Fuise a to na téma Pružnost Pevnost I. Co to znamená pro vás, jako čtenáře? Budou se tu objevovat poznámky, které považuji za důležité a hlavně potřebné ke zvládnutí zkoušky a budu se všemožně snažit je vysvětlit naprosto selským rozumem. Proto vy jedničkáři a dvojkaři – nejspíš se tu budete nudit ^_^
Zdravím potenciální čitatele tohoto blogu. Rozhodl jsem se, alespoň prozatím (dokud mi do toho něco neskočí) navštěvovat přednášky pana docenta Fuise a to na téma Pružnost Pevnost I. Co to znamená pro vás, jako čtenáře? Budou se tu objevovat poznámky, které považuji za důležité a hlavně potřebné ke zvládnutí zkoušky a budu se všemožně snažit je vysvětlit naprosto selským rozumem. Proto vy jedničkáři a dvojkaři – nejspíš se tu budete nudit ^_^
Rozhodně nebudu popisovat vše a naprosto důkladně. Máte chodit na přednášky 🙂 Spíše se budu snažit jen něco dovysvětlit, přiblížit, dát více příkladů a tak. Uvidíme, kam to dopracujem.
Upozorňuji, že PPI i PPII mám zdárně za sebou, tomuto se věnuji z vlastní iniciativy a nechávám si právo to tu kdykoli přestat psát. Tak berte, dokud můžete 🙂 A kdyby se někomu líbil můj styl výuky a chtěl doučování, neváhejte mi napsat, můžeme se domluvit (jsem na Purkyních). Finanční ohodnocení rozhodně nebudu přehánět – spíš méně, než všichni ostatní 🙂
Inu, pusťme se do toho.
První hodina se nesla v duchu klidném, nestresovém, hlavní náplň spočívala v utřídění si základních poznatků, které budeme využívat jak v PPI, tak i v PPII. Také byla oznámena skvělá a pozitivní zpráva z úst pana docenta Fuise: body ke zkoušce nebudou podléhat stupidnímu systému ze zimního semestru, kde to bylo vyzkoušeno na statice.
Pro neznalé: body na cvičení, které jste mohli dostat po úspěšných zápočtech (15-30b) se od 15++ násobily koeficientem 2. Neboli kdo měl 15b ze zápichu, na zkoušce začínal s 0b, kdo 23, na zkoušce začínal s 16b, kdo 28, odnesl si 26b. Prý má systém „více mínusů, než ten minulý“, proto se vracíme ke klasice. Co si odnesete ze zápočtu, máte i u zkoušky.
Pro Letní semestr 2013 budou zápočtové písemky v 5. 9. a 12. týdnu. (tzn týden začínající 4.3, 1.4 a 22.4)
Přednáška >> [PDF] << a její audio nahrávka: PPI Přednáška [1] – 5.2.2013 – Fuis: >> [MP3] <<
V pružnosti i statice existuje několik typů stavů tělesa.
Jedná se o stavy volné, vázané a uvolněné.
• Volné ~ zanedbáváme zde silové působení. Můžeme to připodobnit na zátěž vlastní vahou. Neboli třeba zda se unese sám jeřáb.
• Vázané ~ těleso je zatíženo buď silovou, nebo stykovou vazbou. Silová vazba je jasná, síla působící na nějakém místě či tlak působící na stěny roury. Styková je pak tlak od nějakého styčného tělesa (dvě krychle na sebe působící, míč kopnutý do obličeje malého dítěte.
• Uvolněné ~ kategorie sama pro sebe, ale zkusím to zjednodušit a trochu popsat. Dělí se na úplně uvolněné a částečně uvolněné.
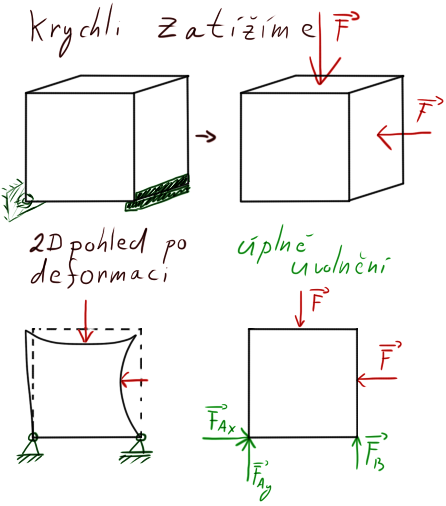
Co je to však uvolnění? Řekněme, že máme těleso (plastová krychle). To zatížíme silou uprostřed a na kraji. Ve výsledku je lehce deformované (střed se prohne). Pokud my toto těleso uvolníme, bude mít stejný tvar jako bez zatížení (nebude prohnuté), protože na něj „nebudou působit síly“, ale ony deformace a síly tam napsat musíme. Neboli tam, kde působily síly, budou i nadále působit síly. Tam, kde se objevila deformace (ono prohnutí středu), zavedeme nějakou deformaci (posun = 0,5mm / prodloužení = 2mm)
• Úplně uvolněné ~ vyskytuje se jak v pružnosti, tak i ve statice (tam prioritně). Jak jistě víte, pro 2D těleso máme 3 možné podmínky, a to Síly ve směru $x$ a $y$ a poté Moment kolem osy z. Ve 3D je však podmínek 6. 3 Síly $(F_x, F_y, F_z)$ a odpovídajícně 3 Momenty $(M_x, M_y, M_z)$.
Pokud si tedy vezmu těleso ve 2D, které je uchyceno posouvající vazbou (odebírá 2 stupně volnosti) a rotační vazbou (odebírá 1 stupeň volnosti), v těchto vazbách vzniknou 3 neznámé parametry, které dosadím do podmínky, že Stupeň volnosti = počet neznámých – počet možných. Pokud dostaneme číslo 0, jsme z obliga, nečeká nás žádný Castiglian, žádné složité přemýšlení a doděláme lehce příklad. Pokud nám vyjde číslo 1 (počet neznámých převyšuje počet možných) či nedejbože víc!, nastává částečné uvolnění.
• Částečně uvolněné ~ vyskytuje se jen v pružnosti (ve statice jsme jen napsali, že to není možno řešit). Pokud počet neznámých převyšuje počet možných, částečné uvolnění je pak nahrazení jedné neznámé (dle naší osobní preferované volby) nějakou vazbou a! přidáním deformační podmínky. Poté opět úplně uvolníme na úroveň statické určitosti (počet neznámých = počet možných) a řešíme problém.
Co tím míní básník říci? Pokud je těleso uchyceno v rotační vazbě, částečným uvolněním přeměníme tuto rotační vazbu na vazbu posuvnou (nebo vetknutí na vazbu rotační (+ moment) nebo posuvnou odstraníme úplně (+ síla)) a do onoho místa umístíme sílu s deformační podmínkou (v tomto případě vertikální / horizontální posuv = 0). U vetknutí by částečné uvolnění probíhalo jako nahrazení rotační vazbou a deformační podmínkou k momentu, že natočení = 0.
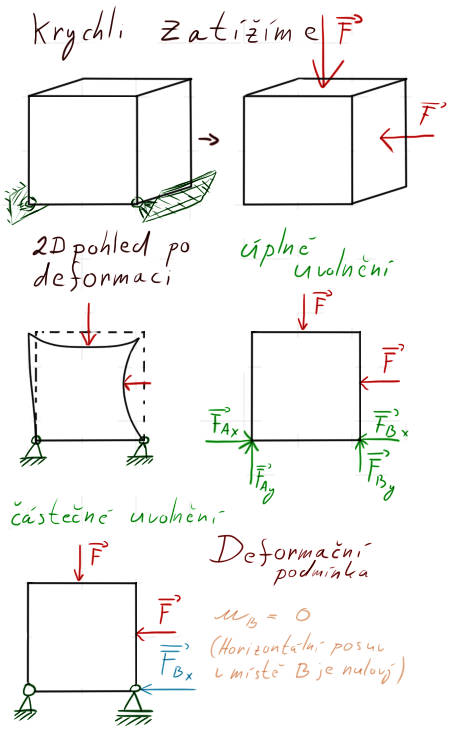 Prakticky všechny problémy Pružnosti Pevnosti I a II začínají právě na tom, že je těleso staticky neurčité, provedete částečné uvolnění, nahradíte jednu, dvě, tři vazby známou deformační podmínkou (ať už , či třeba nějaké známé natočení / posuv / prodloužení), ze které zjistíte onu jednu sílu/moment v částečně uvolněné vazbě a dopočítáte další neznámé z rovnic rovnováhy $(\sum{F_x=0}, \sum{F_y=0}, \sum{M_z=0})$. Další úkony jsou pak vcelku snadná záležitost.
Prakticky všechny problémy Pružnosti Pevnosti I a II začínají právě na tom, že je těleso staticky neurčité, provedete částečné uvolnění, nahradíte jednu, dvě, tři vazby známou deformační podmínkou (ať už , či třeba nějaké známé natočení / posuv / prodloužení), ze které zjistíte onu jednu sílu/moment v částečně uvolněné vazbě a dopočítáte další neznámé z rovnic rovnováhy $(\sum{F_x=0}, \sum{F_y=0}, \sum{M_z=0})$. Další úkony jsou pak vcelku snadná záležitost.
A jaký je vlastně cíl tohoto počítání?
Predikce mezních stavů (deformací / porušování) a jejich případná rekonstrukce (kde že je chybka).
Mezní stavy [MS]
Mezní stavy můžeme rozdělit do dvou kategorií. Jsou to stavy deformační a stavy související s porušováním.
Mezní stavy deformační
MS deformace: Deformace funkčně přístupné se dotknout hranice funkční nepřípustnosti. Co to znamená v češtině? Pokud půjdu nad sopkou přes dřevěnou lávku a vím, že pokud se prohne o více jak 3 metry dolů, shořím v plamenech. MS deformace budou ony 3 metry. Pokud se prohne o míň, je to v pořádku, pokud o víc, pozdravíte Satana.
Reálnější příklad: Mám větráček od procesoru (rotor) otáčející se uvnitř plastového rámečku (stator) a vůle mezi lopatkami a rámečkem je 1mm. Pokud se ať už vlivem trhliny, rychlosti nebo teploty lopatky dotknou rámečku, nastal MS deformace. Přípustná se změnila v nepřípustnou.
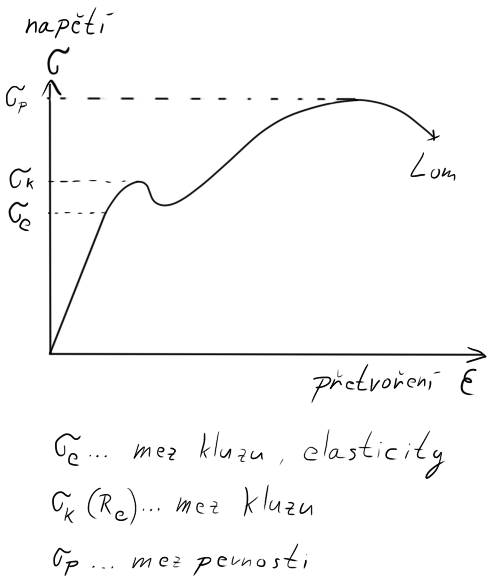
MS pružnosti: Pamatujete na předmět Struktura Materiálů a na křivku vynesenou v grafu $\sigma – \varepsilon$? Ne? Nebojte, nachází se pod textem. Jak vidíte, pokud na materiál působím nějakou silou, deformuje se (prodlužuje – $\varepsilon$). Až po mez kluzu (značící se $R_m$ / $\sigma_k$) jde o deformaci pružnou. Pokud materiál přestaneme zatěžovat, vrátí se do původního stavu a vo to nám jde. Pokud by se mez pružnosti/kluzu/elasticity (synonyma) překročila, vzniknou v materiálu makroskopické deformace, které jsou příčinou skluzu atomových rovin, což je smykové napětí, což je špatné… O tom někdy později. Zkrátka a jednoduše, nechceme, aby materiál přešel z elastického stavu do plastického / nechceme, aby překročil mez kluzu.
MS deformační stability: Stav tělesa, při jehož dosažení se jeho geometrická konfigurace, která byla stabilní, stává labilní a stabilní konfigurací se stává jiná geometrická konfigurace.
Česky řečeno: Pokud mám železniční koleje, které jsou díky vedru a dalším vlivům rozpínány, tak se něco najednou zvrtne a z původních rovných (původní geom. konf.) se koleje stanou vybočené na stranu (výsledná geom. konf.). Z jedné „podoby“ se to změní -nežádoucně- na „podobu jinou“.
Tento MS se pak dělí na další:
MS vzpěrné stability: Na to jsou speciální vzorečky a speciální kategorie sama pro sebe. Někdy to rozvedu, dnes ne. Jde o to, že pokud působíte silou na nějaký sloup, teoreticky by měl vydržet (MS pružnosti / MS deformace), ale z nějakého divného důvodu to křupne, vybočí a zboří se celá budova.
MS klopení nosníku
MS boulení stěn
MS stability skořepin
Mezní stavy související s porušováním
MS porušení spojitosti: koukám na materiál a najednou… „Hele, trhlina O.o“.
MS trhlin [PPII]: Viděl jsem sice trhlinu, ale byla v pohodě. Nerostla, nebo rostla extrémně pomalu. Protože, jak je obecně známé, prakticky neexistuje těleso -bez trhlin- (krom speciálně vyrobených diamantů a super úžasných krystalů), jsme na ně zvyklí, tolerujeme je. Tento mezní stav nám však říká, že trhlina dospěla do takového stavu / velikosti, že se pro nás stala funkčně nepřípustnou.
MS stability trhlin: Tento stav závisí s proměnným zatěžováním. V okamžiku, kdy soustavě dodávám nějakou energii (síla / tlak / změna teploty), trhlina roste. O tom žádná pře (až na výjimky, ale to ponechme teď stranou). Ale co se stane, pokud těleso přestanu namáhat, neboli trhlině odeberu dodávanou energii? Pokud se taková trhlina přestane šířit, je to v pořádku. Pokud se však šířit nepřestane a samovolně se stále zvětšuje, roste, můžeme říct, že nastal MS stability trhliny -> trhlina už není stabilní (je nestabilní 🙂 )
MS lomu: Jak už název evokuje, MS nastane v okamžiku lomu. Jaké lomy však můžou nastat?
• křehký lom [PPII] ~ stačí pouze malá spotřeba energie na malé deformaci a nastane lom
• tvárný/houževnatý lom ~ je potřeba mnoho energie
• creepový ~ při konst. teplotě a míjivém / pulzujícím charakteru zatěžování v tahu za vzniku jednosměrného nárůstu plastické deformace (o mnoho rychlejší než únavový lom)
• únavový lom [PPII] ~ vzniká cyklickým zatěžováním, jde buď o nízkocyklovou či vysokocyklovou únavu a dále se dělí na:
Mechanická únava ~ střídavé silové (mechanické) zatěžování za normálních, zvýšených či snížených teplot
Tepelná únava ~ střídavá změna teploty tělesa
Tepelně mechanická únava ~ jak jistě předpokládáte, spojení obou výše uvedených (tyč zaražená mezi dva bloky je ohřívána, ale nemá se jak roztáhnout, takže tam vzniká jak teplotní, tak i mechanická zátěž)
Wou! Těch je… To se to budem muset naučit všechno?
Ale kdeže 🙂 Takový MS lomu se učí v prvních týdnech Pružnosti Pevnost II, to stejné platí i o MS spojených s trhlinami.
V Pružnosti Pevnosti I budeme zkoumat tyto mezní stavy:
• MS pružnosti (aby to nepřekročilo mez kluzu $(R_m/\sigma_k)$ )
• MS deformace (aby to nepřekročilo zadanou vzdálenost, prohnutí)
• MS vzpěrné stability (protože i když to vydrží MS pružnosti i deformace, je možné, že se nám to stejně posere 🙂 )
To by bylo k uvolnění a mezním stavům. Co nás čeká dále?
Pan docent Fuis (mmj dle mého názor vysvětluje lépe a srozumitelněji (selsky) než pan profesor Vrbka. Na druhou stranu mít Vrbku na zkoušku je odměna, než nesnáz. U Fuise jsem dělal statiku natřikrát.) dále trochu načal otázku typu napětí (normálové / smykové) a tenzorů. Proto jen lehce k tomu.
Napětí, tenzor napětí a tak
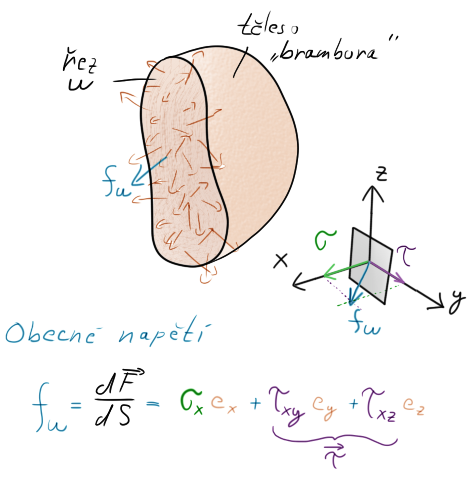
Pokud máme nějaké těleso, které zatížíme a rozsekneme ho libovolně zakřiveným řezem, můžeme v jeho vnitřnostech pozorovat nějaké síly a momenty, resp napětí. Je jich nekonečně mnoho v nekonečném množství nekonečně malých bodů.
Řekněme ale, že si zvolíme jeden bod a tomu bude náležet (víc jich nemá) jedno obecné napětí. Názorná grafika pro představu.
Jak vidíte, toto napětí (! kolmé k řezu $\omega$)! se skládá z napětí hlavního sigma ($\sigma$) (kolmém na řez) a smykového tau ($\tau$) (rovnoběžného s řezem).
Pokud však chceme popsat naprosto jednoznačně napjatost v jakémkoli bodě v 3D prostoru, nepotřebujeme k tomu nekonečné množství rovnic a parametrů, ale stačí nám zvolit si v onom bodě 3 roviny navzájem na sebe kolmé. Čím takové roviny budou charakteristické?
• můžeme je popsat 3 hlavními napětími, které budou kolmé na ony roviny
• a dále zde bude 6, potažmo 3 smyková napětí, které budou vždy rovnoběžné s 2, potažmo 1 rovinou a kolmé na třetí. (bude vysvětleno později)
Tento stav můžeme popsat následovně:
Tenzor obecného napětí:
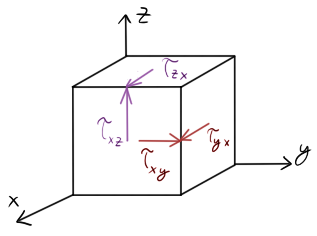
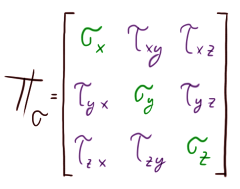 Hlavní napětí (zeleně) existují v jednom bodě tři. Jsou velmi žádaná, usnadňují nám život a pečou koláče. Dále zde máme 6 smykových napětí (fialově), které mají krásnou vlastnost, vždy do diagonály mají stejnou velikost. Neboli: $\tau_{xy} = \tau_{yx}$. Proč se tedy značí $xy$ / $yx$?
Hlavní napětí (zeleně) existují v jednom bodě tři. Jsou velmi žádaná, usnadňují nám život a pečou koláče. Dále zde máme 6 smykových napětí (fialově), které mají krásnou vlastnost, vždy do diagonály mají stejnou velikost. Neboli: $\tau_{xy} = \tau_{yx}$. Proč se tedy značí $xy$ / $yx$?
1. index ~ normálová rovina, na které smykové napětí působí
2. index ~ směr, kam smykové napětí působí
Obrázek za tisíc slov:
To by bylo pro dnešek vše, příště se na to podíváme podrobněji.

2 responses to “PPI – 01 – úvodní hodina”