Dneska to bude konečně zajímavější, zabředneme do tajů věty, která nás bude provázet po celou PPI a dokonce i polovinu PPII.
Čeká nás nějaká ta charakteristika věcí (lineární pružnosti), se kterými budeme počítat, Bettiho věta popisující ledabylost postupu zatěžování (pokud chceme počítat jen s finálním tvarem), naprosto úžasná Castiglianova věta, která nám řeší jakoukoli staticky neurčitou prutovou úlohu a můžeme s ní spočíst průhyby, posunutí či natočení v kterémkoli místě prutu a nakonec si řekneme, co to ten prut je.
I když… Proč tím nezačít 🙂
Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [3] – 12.2.2013 – Fuis: >> [MP3] <<
Prut
Prut je těleso, které se popíše pomocí několika různých charakteristik, a to:
• Jeden rozměr je mnohonásobně větší, než zbylé dva rozměry (délka je metr, průměr centimetr)
• Průřez tělesa je spojitý (není přerušený), souvislý
• Průřezy zůstávají po deformaci stále kolmé na střednici
Stavy průřezů: (o těchto stavech bude zbývající několikatýdenní učivo)
• oddalují se / přitahují se … $N$
• natáčejí se kolem osy ležící na průřezu a deformují se … $M_o$
• natáčejí se kolem osy kolmé k průřezu a NEdeformují se … $M_k$
• posouvají se bez deformace … $T$
• Všechny zatížení a vazby působí pouze na střednici (ne na povrch tyčky)
• Napjatost v bodě prutu je dána normálovou a smykovou složkou obecného napětí v příčném průřezu.
Co vše je nutné splnit
• Okrajové Podmínky musejí být lineární
(OP ~ vazby / zatížení), zde platí:
a) odchylky jsou nepodstatné
b) lineární závislost mezi zatěžujícími vazbami a deformačními posuvy
$u = c \cdot F$ | ($c$ … poddajnost) $[mN^{-1}]$
$u = F / k$ | ($k$ … tuhost) $[Nm^{-1}]$
c) lineární vazby
• Materiál musí být lineárně pružný
(neboli jsme schopni počítat až (jen) do meze kluzu)
• Napjatost nezávisí na historii zatěžování
(neuvažujeme tedy zbytkovou napjatost, která se v materiálu velmi často vyskytuje)
• V tělese jsou malé deformace … jsou ostře menší, než rozměry tělesa
poměrné přetvoření normální $\varepsilon < 1 %$
poměrné přetvoření u MKP $\varepsilon < 5 %$
Bettiho věta
Nyní, když víme, co je prut a jaké musí mít vlastnosti (což bychom měli vždy v úloze překontrolovat, protože stačí, aby neplatila jen jedna vlastnost a už nemůžeme aplikovat následující výpočty a teorie), se pustíme do zábavnějších věcí 🙂
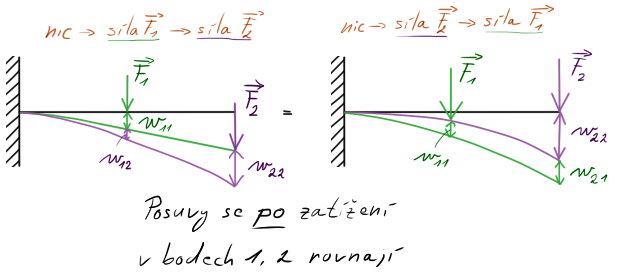
Co by se stalo, kdybychom zatěžovali vetknutý nosník nejprve silou $F_1$ a poté přidali $F_2$?
Co by se stalo, kdybychom napřed zatěžovali silou $F_2$ a poté přidali $F_1$?
Jaký bude průběh? Jaký bude výsledek?
Výsledek bude naprosto totožný. Je jasné, že pokud bych zatěžoval silou $F_1$ a změřil posuv jak v bodě 1, tak 2, budou jiné, než když bych zatížil jen silou $F_2$.
Dokonce i průběh zatížení bude jiný.
Ale ve finálním stavu, kdy naplno působí obě síly, vůbec nezáleží na pořadí zatěžovacích sil.
Bettiho věta. To je vše 🙂
Castiglianova věta
Tak a je to tady. Dle mého jedna z nejdůležitějších vět celé Pružnosti Pevnosti I a půlky PPII. Pokud se jí naučíte, dobře pro vás. Pokud ne, můžete se rozloučit se zkouškou z PPI, PPII, protože Castigliana použijete prakticky všude.
Co to tedy je? Jak se k tomu dostat? Aneb trocha teorie.
Pokud máme nějaké těleso a působíme na něj silou, tato síla koná práci.
Z předešlé teorie víme, že posuv je lineárně závislý na síle.
• Neboli: $u = c \cdot F$ či $u = \dfrac{F}{K}$ … využijeme první vztah, kdy se počítá s poddajností $c$.
• Pokud tedy síla koná práci, koná ji na nějaké délce.
• Pokud přidáme integrál, práce se nám změní v přírůstek práce. $\displaystyle A = \int_{0}^{u_k}dA$
• Onen přírůstek práce se dá napsat jakožto síla násobená přírůstkem posunutí. $dA = F \cdot du$
• Sílu můžeme vyjádřit právě díky vztahu uvedeném výše. $F = \dfrac{u}{c}$
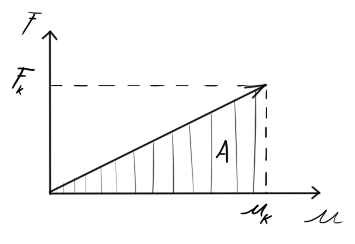
• Vzejde nám výsledný tvar integrálu po nějaké délce (od $0$ do $u_k$) obsahující posunutí násobené přírůstkem posunutí, to vše podělené konstantou poddajnosti. $${A = \frac{1}{c} \cdot \int_{0}^{u_k} u \cdot du = \frac{1}{2} \cdot F_k \cdot u_k}$$ kde $u_k [mm]$ je deformační posuv na konci stavu, kdy působí síly.
Celé se to dá o dost krásněji vyjádřit za pomocí grafu:
 U momentu je to prakticky stejná záležitost. $A = \dfrac{1}{2} \cdot M \cdot \varphi$
U momentu je to prakticky stejná záležitost. $A = \dfrac{1}{2} \cdot M \cdot \varphi$
Castiglian je obecná metoda pro určování deformací
Pokud se nachází těleso ve statické rovnováze (počet neznámých = počet možných), stačí mi bohatě pro popis (v bodě $A$ v SS $x-y$) 3 rovnice
$$\sum F_{x} = 0$$
$$\sum F_{y} = 0$$
$$\sum M_{ZA} = 0$$
Pokud má však těleso neznámých více (moc podpor např.), než počet možných, říkáme o něm, že je staticky neurčité.
Stupeň statické neurčitosti $S$ je jednoduše: S = neznámé – možné.
Jestli tedy mám $S = 1$, neboli „jedenkráte staticky neurčité“, musíme zavést tzv. deformační podmínku, která nám charakterizuje stav ve zvoleném bodě, o kterém něco víme a který nám dožene ony neznámé a pomůže vše vyřešit.
(pokud by bylo $S = 2$, musíme mít 2 deformační podmínky atd)
Deformace = posunutí / natočení.
Pokud na to jdeme z mikroskopického hlediska, půjde o diferenciály, neboli nekonečně malé posuvy. Diferenciály jsou spojeny s derivací.
Pokud si tedy vezmeme na grafu bod $A$, jehož souřadnice známe, jak zjistit souřadnice $x, y$ (resp. třeba posunutí ve směru $y$) bodu $B$?
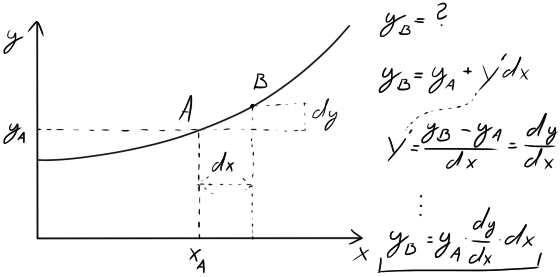 Představme si nyní zatížené těleso různými momenty, silami, působeními a my chceme zjistit, jaký je posuv v jednom bodě a námi určeném směru. Nejlépe třeba ve směru $z$ (kolmo na $x$, směrem dolů).
Představme si nyní zatížené těleso různými momenty, silami, působeními a my chceme zjistit, jaký je posuv v jednom bodě a námi určeném směru. Nejlépe třeba ve směru $z$ (kolmo na $x$, směrem dolů).
Práce $A$ je funkcí sil $F_1$, $F_2$, …, $F_i$, ovšem my chceme jen směr posunutí v jedné síle.
Platí tedy 2 rovnice.
První nám říká, čemu se rovná práce, druhá nějaké ty spojitosti mezi silami a posunutím. Pokud v těchto rovnicích porovnáme práci, vyjde nám po vykrácení… … bla bla.
Přeskočme však nudnou teorii a vrhněme se na extrémně důležité rovnice:
• Posuv ve směru síly $F_i$ je roven parciální derivaci energii napjatosti podle oné síly.
$$u_i = \frac{\partial W}{\partial F_i}$$
• Natočení v místě momentu Mi je rovno parciální derivaci energii napjatosti podle onoho momentu.
$$\varphi_i = \frac{\partial W}{\partial M_i}$$
O energii napjatosti se pobavíme nejspíše příště (jde jen o to sečíst všechnu energii napjatosti ve všech intervalech tělesa / soustavy těles), ale nejprve ještě „oficiální definice“ výše uvedených rovnic.
Deformační posuv působiště síly $F$ po její nositelce je dán parciální derivací celkové energie napjatosti tělesa (soustavy) podle této síly.
Úhel natočení v místě působení silové dvojice je dán parciální derivací celkové energie napjatosti tělesa (soustavy) podle této silové dvojice.
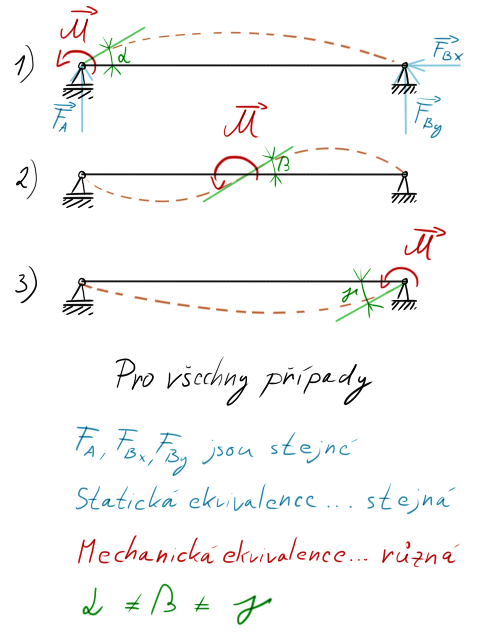
Jak jsme byli zvyklí ve statice, že je nevýznamná poloha momentu, zde nabývá velkého smyslu. Ukažme si to to na jednoduchých třech případech, kdy budeme posouvat působiště po prutu.
Doplňkové síly
Jak už jsme si řekli, pokud bychom chtěli v libovolném bodě zjistit posuv či natočení prutu, musíme parciálně zderivovat energii napjatosti celého tělesa podle působící síly / momentu ve směru či bodě, který nás zajímá.
Co když tam však žádná síla působit nebude?
Pokud bychom měli vetknutý nosník a zajímal by nás posuv někde uprostřed, kde nepůsobí síla, musíme v onom bodě zavést sílu doplňkovou $F_{dop}$ a položit její velikost nule.
Grafické znázornění pro lepší pochopení:
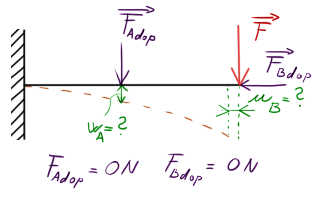 A co kdybychom chtěli zjistit úhel natočení v bodě $A$ nebo $B$? Vložíme na ona místa doplňkový moment $M_{dop}$ a položíme ho $0 Nm$.
A co kdybychom chtěli zjistit úhel natočení v bodě $A$ nebo $B$? Vložíme na ona místa doplňkový moment $M_{dop}$ a položíme ho $0 Nm$.
Posunutí v bodě $A$, resp. $B$ tedy bude $w_A = \dfrac{\partial W}{\partial F_{A_{dop}}}$, resp. $u_B = \dfrac{\partial W}{\partial F_{B_{dop}}}$, natočení $\varphi_A = \dfrac{\partial W}{\partial M_{A_{dop}}}$
Dodatek
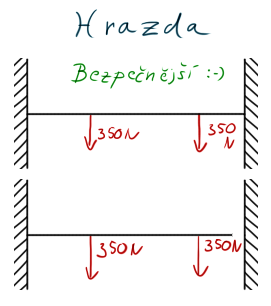
Proč vlastně existují staticky neurčité úlohy? A kolikrát i více než jednou? (mají o dost více neznámých než možných)
• Snižují napjatost
• Zvyšují bezpečnost
Prakticky všechny řešení v reálném životě jsou staticky neurčité. Pokud byste měli mezi dveřmi hrazdu zaraženou jen jedním koncem, vcelku bych se bál na tom cvičit. Ovšem pokud ji zarazíte i druhým koncem, stane se z ní úžasný cvičící nástroj. Jenže je 3x staticky neurčitá 🙂
Tak to je vážení pro dnešek vše a pokračujem ve čtvrtek / pátek 🙂