„pokračování“ úvodní hodiny je zde a je na čase dodělat první přednáškové pdf.
Co se tedy dnes přiučíme, co si vlijeme do hlavy? Minule jsme probírali velmi zkráceně napětí. Dnes probereme velmi zkráceně deformaci, na kterou má přímý vliv ono napětí, poté vztahy, které se mezi nimi dají napsat (zvané konstitutivní), přiblížíme si Saint-Venantův princip a podíváme se na náznak výpočtů bezpečnosti. Pod čarou se pak kouknem, co jsme vlastně schopni analyticky (perem a tužkou) spočíst.
Vrhněme se do toho! 🙂
Přednáška >> [PDF]<< a její audio nahrávka: PPI Přednáška [2] – 7.2.2013 – Fuis: >> [MP3] <<
Pokračování z napjatosti
O napjatosti v tělese by se toho dalo napsat mraky, ale zdůraznil bych zde jednu šikovnou věcičku. Je to také zkoušková otázka na teorii.
Sdruženost smykových napětí
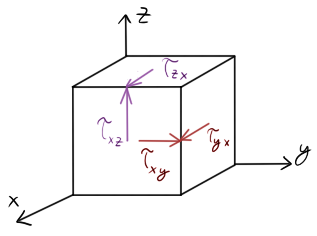
Pokud si vybavíte krychličku z minula (nekonečně malý elementární prvek), působí na ni 4, potažmo 2 smyková napětí. Co to tedy znamená to potažmo.
Pokud bychom si vzali krychličku velkou, řekněme jako jablko a působili z jedné strany $\tau_{yx}$, dovedeme si jistě představit, že z druhé strany bychom mohli $\tau_{xy}$ tlačit též, ale asi to nezvládneme stejně velkou silou. Pokud si ale vezmeme nekonečně malý element a sílu tedy budeme vykonávat na nekonečně malé plošce, můžeme vyslovit zákon o sdruženosti smykových napětí, a to:
Pokud ve dvou na sebe kolmých rovinách (např. x, y) působí smyková napětí, jsou pak tyto smyková napětí stejně velká a jejich směr je buď k sobě (k průsečnici), nebo od sebe.
Znaménková konvence nám říká, že
• pokud směřují smyková napětí k sobě … +
• pokud směřují smyková napětí od sebe … –
Platí ale pouze pro malé deformace.
Deformace
Co to vlastně jde? Je to množina deformačních posuvů v nekonečně bodech tělesa.
Pokud bychom měli jablko skládající se ze 2 milionů bodů, jeho deformace (ať už promáčknutí či jen přesunutí v prostoru následkem jiné síly) by byla výsledkem součtu každého z těch 2 milionů posuvů. Jeden by šel přímo doprava, druhej lehce šikmo dolů atd…
Abychom si to alespoň lehce přiblížili, budeme deformovat (2D) čtvercovou mřížku.
Pokud bychom tedy chtěli vyjádřit posuv v bodě, kde působí síla (viditelně největší posuv), musíme spočíst posuvy v naprosto celém tělesu. Což zavání nějakou sumou, případně integrálem. To nás však čeká až v nějakém 4? týdnu, takže času dost 🙂
Opět zde funguje nějaká konvence, pro posuvy tedy platí:
• osa x … $\vec{u}$
• osa y … $\vec{v}$
• osa z … $\vec{w}$
Převoření
Deformace je úzce spolčená také s pojmem přetvoření. To může být jak poměrné (lineární čáry), tak úhlové (natočení)
Poměrné přetvoření ~ většinou vyvolané normálovými silami
Vzorec pro vypočtení poměrného přetvoření je jen porovnání jeho nové délky k délce staré, neboli:
$$\varepsilon=\frac{\Delta l}{l}$$
↑ platící pro konečnou dráhu (předmět, kde známe délku) ↑
↓ platící pro malé (elementární) přetvoření ↓
$$\varepsilon_x=\frac{dx^{\prime}-dx}{dx}=\frac{du}{dx}$$
Úhlové přetvoření ~ většinou vyvolané smykovými silami

Zelená: jen jedno smykové napětí
Červená: jen jedno smykové napětí
Modrá: přetvoření z obou napětí naráz
Přetvoření úhlové je jednoduché od pohledu. Odečteme od 90° onen úhel $\varphi$.
$$\gamma_{xy}=\frac{\pi}{2}-\varphi_{xy}^{\prime}$$
Přetvoření obecné se pak dá napsat jako:
$$\mathbb{T}_{\varepsilon} = \begin{bmatrix}
\varepsilon_x & \dfrac{\gamma_{xy}}{2} & \dfrac{\gamma_{xz}}{2} \\
\dfrac{\gamma_{xy}}{2} & \varepsilon_y & \dfrac{\gamma_{yz}}{2} \\
\dfrac{\gamma_{xz}}{2} & \dfrac{\gamma_{yz}}{2} & \varepsilon_z
\end{bmatrix}$$
Konstitutivní vztahy
Aneb ~ vztahy mezi napětím a přetvořením. (matematicky – mezi jejich tenzory)
Nejprve by se slušelo zmínit, na co nám vlastně budou.
Jedná se o vztahy, které nám díky přetvoření zjistí napjatost, která v daném bodě a daném směru působí. Také (logicky i opačný směr) nám zjistí přetvoření na základě toho, jakou na bod působím napjatostí.
No není to úžasné, Time? Rozhodně!
„Jak se tedy těmto zákonům říká a proč jsem o nich ještě neslyšel?“
Z fyziky „jistě známe“ Hookův zákon. Toto je to samé v bledě modrém.
Existuje několik tvarů.
Obecný tvar

Tenzor napětí = Matice tuhosti materiálu * Tenzor přetvoření
Mat. tuhosti: až 81 konstant!
Při izotropním materiálu však jen 2. (Modul pružnosti $E$ a Poissonova konstanta $\mu$)
No, … na první pohled je to šílenost, ale jak už to v matice, fyzice a dalších předmětech bývá, z obecného tvaru škrkneme mrtě věcí, které nepovažujeme za důležité nebo potřebné / vlivné a zajímavé.
Zbude nám tedy (mathica magicka):
Zobecněný tvar
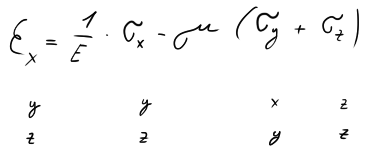
PLATÍ JEN !! V oblasti Elastických Přetvoření.
Pokud bychom se nacházeli v oblasti plastických deformací (materiál se po namáhání určitou silou NEvrátí do původního stavu), tento vzorec NEPLATÍ.
Co s tímto vzorcem? Vzpomínáte na krychličku nahoře? Vezměme si, že ji zatížíme ze všech stran nějakou tahovou silou. Aby se přetvářela tak, jak je nahoře zobrazeno. Prodloužení ve směru $x$ se tedy spočte za pomocí $\sigma_x$, $\sigma_y$ a $\sigma_z$.
(V případě, že by byla krychlička zatížena jen jedním / dvěma, tak se vzorec ještě zjednodušší).
Ale to ještě není všechno!
Tento zákon můžeme dále zjednodušovat 🙂
Pokud se jedná o:
• jednoosou napjatost,
v češtině více známou (tlačím či tahám jen v jednom směru, a to ještě kolmém na nějakou osu), je přetvoření přímo úměrné napjatosti.
V matematickém slangu to vypadá: $\sigma_x = E \cdot \varepsilon_x$
• rovinnou smykovou napjatost,
v češtině více známou (v jedné rovině působí smyk, takže tam jsou ty 2 sdružená napětí o stejné velikosti), je úhlové přetvoření přímo úměrné smykové napjatosti.
A opět matematické hledisko: $\tau_{xy} = G \cdot \gamma_{xy}$
Další pojmy a vzorečky, které je záhodno (ale NENÍ tak nějak úplně NUTNO) si pamatovat:
$E$ … modul pružnosti
Pro ocel: 210 000 MPa
$\mu$ … Poissonova konstanta
$$\mu_{xy} = – \frac{\varepsilon_y}{\varepsilon_x}$$
$$\mu_{xz} = – \frac{\varepsilon_z}{\varepsilon_x}$$
$G$ … modul pružnosti ve smyku
$$G = \frac{E}{2 \cdot (1 + \mu)}$$
Saint Venantův princip
Než se pustíme do vysvětlování, k čemu tato (opět) zkoušková testovací otázka je a proč je prospěšná?
Pojďme do historie.
Pan Venant tuto myšlenku, chcete-li tézi, přednesl v roce 1855, kdy se nemohlo dostupnými metodami tvrzení ani potvrdit, ani vyvrátit. Nikdo si nedovolil pochybovat (ti co pochybovali si to nechali pro sebe) a dobře udělali. V roce 1945 se lidé konečně dočkali: s údivem a určitým respektem bylo Saint Venantovo tvrzení potvrzeno. O co se tedy jedná?
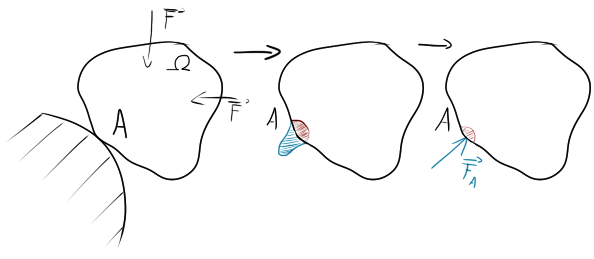
Nahradíme-li silovou soustavu působící v bodě A jinou staticky ekvivalentní silovou soustavou, pak bude napjatost tělesa v obou systémech prakticky stejná s výjimkou blízkého okolí bodu A.
Vizuálně by se to dalo zobrazit takto:
Pro nás to znamená následující. Pokud budeme mít liniové zatížení, můžeme ho nahradit silou bodovou (ale staticky ekvivalentní). To samé i pro ostatní typy sil.
Bezpečnost
Co vyrozumět pod tímto pojmem? Cílem PP je, jak už bylo řečeno v první lekci, něco ve smyslu „hele, kdy nastane mezní stav a kolik že to teda vydrží?“
Bezpečnost tedy porovnáváme s nějakým maximem, které se většinou značí $\sigma_{k}$ nebo $R_{e}$.
Bezpečnost jako takovou označujeme $K$ a je to podíl nějakého toho maxima (mezní hodnota) vůči nějaké námi vypočítané maximální provozní (či montážní) hodnotě.
Zní to komplikovaně, ale není 🙂 Prostě porovnáme maximální možnou hodnotu s jiným maximem, které najdeme díky výpočtům.
Pokud nám onen poměr, bezpečnost $K$, vyjde větší než 1, je to v klidu. Pokud menší, je tam průšvih.
Jaké jsou tedy typické bezpečnosti?
Optimální leží mezi 1,5 ~ 1,7 (max tak 2). K Meznímu stavu pevnosti (po překonání tohoto MS se těleso rozlomí) je při této bezpečnosti stále mnoho místa. Protože i pokud se těleso plasticky deformuje, pořád ještě může dlouhou dobu v pořádku fungovat. Vše záleží na „dovolené míře“.
Jen tak pro zajímavost, výtah (lano třeba) se počítá na bezpečnost blízké $K=10$. Protože zde předpokládáme, že i malá plastická deformace by mohla být průser (neboli ono zatížení 350Kg / 5 lidí v kabině by zvládlo možná i tunu, ale pro několikadesetiletý bezchybný provoz je tam limit oněch 350Kg. „Nové“ výtahy se ani nerozjedou, pokud se nějaká hmotnost překročí).
Něco k počtech. Bezpečnost na:
Mezní stav pevnosti:
ohyb: $K_k = \dfrac{\sigma_{k}}{\sigma_{max}}$
smyk: $K_k = \dfrac{\tau_{k}}{\tau_{max}}$; $\tau_{k}$ bývá většinou $2\sigma_k$
Mezní stav deformace:
$$K_D = \dfrac{u_{mezni}}{u_{max (provozni)}}$$
Dovolené napětí: inverzní úloha. Máme tedy danou bezpečnost např. $K = 1,7$, maximální zatížení a máme spočíst dovolené (ve vzorcích nahoře pomocí $K_{k}$ a $\sigma_{k}$ vypočteme $\sigma_{max}$ a tak)
Tento druh příkladů (dovolené napětí) se využívá k určení průměru prutu při bezpečnosti a max. napětí. Nebo určení profilu / tloušťky / délky / teplotní zátěže a podobně.
Něco málo pod čarou k Modelování
Statika – základní geometrie, vazby, zatížení
Pružnost Pevnost I – vruby, průřezy, typ materiálu ($E, \mu, \sigma_{k}$)
Pružnost Pevnost II – jakost povrchu, tepelné zpracování, MS stability, MS únavy, MS trhliny, parametry trhliny a další
Co jsme tedy schopni zpracovat s propiskou v ruce a šálkem kafe v žaludku?
• Analytické modely
Prut (celá PPI, půlka PPII)
Válec, rotačně symetrická deska, rot. sym. stěna, rot. sym. momentová a bezmomentová skořepina (druhá půlka PPII)
A tím to hasne. Pokud máme materiál nehomogenní (dřevo / špatně zpracovaná ocel / další nepravidelné struktury materiálu), nebo to není prut či rotačně symetrické jednoduché těleso (petlahev, plechovka, víko, DVD disk, trubka / roura), jsme v prdeli… Proto tedy nastupují:
• Matematické modely (MKP, alias Metoda Konečných Prvků)
V těchto modelech můžeme řešit teoreticky i prakticky vše. I Méďa Béďa prostřelený šípem by se zde našel. Největší problém je vyhledat potřebné materiálové charakteristiky (modul pružnosti ($E$), modul pružnosti ve smyku ($G$), Poissonovu konstantu ($\mu$) a další konstanty), ale jakmile na ně přijdeme (z praktických testů materiálu ve zkušebnách, z příruček ke známým materiálům, …) a správně zavedeme vazby (upevnění) a zatížení, můžeme pár hodin (crash testy aut) / týdnů či měsíců (u extrémních úloh) počítač nechat bez dozoru a on nám bude žhavit výsledek.
Programy na takové věci jsou třeba ve škole používaný Ansys (další třeba Pam-crash, Nastran), ale o tom někdy jindy.





2 responses to “PPI – 02 – napětí, deformace a bezpečnost”